1  Manipulation des données spatiales dans R

Dans ce chapitre, nous décrivons comment importer, manipuler et cartographier des données spatiales dans R. Pour une description plus détaillée du langage de programmation R – objets et expression, opérateurs, structures de données (vecteurs, matrices, arrays, DataFrame), importation et manipulation de données –, lisez le chapitre intitulé Prise en main avec R (Apparicio et Gelb 2022).

Liste des packages utilisés dans ce chapitre

• Pour importer et manipuler des fichiers géographiques :
  • sf pour importer et manipuler des données vectorielles.
  • rmapshaper pour simplifier des géométries en conservant la topologie.
  • terra pour importer et manipuler des données raster.
  • gpx pour importer des coordonnées GPS au format GPS eXchange Format.
  • foot pour créer des enveloppes orientées sur les géométries.
  • concaveman pour créer des enveloppes concaves.
• Pour cartographier des données :
  • ggplot2 est un package pour construire des graphiques qui peut être aussi utilisé pour visualiser des données spatiales.
  • tmap pour construire des cartes thématiques.
  • RColorBrewer pour construire une palette de couleur.
  • ggpurb pour combiner des graphiques et des cartes.
• Pour importer des tables attributaires :
  • foreign pour importer des fichiers dBase.
  • xlsx pour importer des fichiers Excel.

Pas de panique!

Ce document comprend de nombreuses notions sur l’importation, la manipulation et la cartographie de données spatiales dans R, soit des opérations que vous avez l’habitude de réaliser dans ArcGIS Pro ou QGIS.

Prenez le temps de lire ce premier chapitre à tête reposée et assurez-vous de bien comprendre chaque notion avant de passer à la suivante. L’objectif n’est pas de maîtriser parfaitement la syntaxe R pour toutes les opérations dès la première semaine!

Vous allez manipuler de nombreuses données spatiales avec R au fil de la lecture du livre. Par conséquent, n’hésitez pas à revenir sur ce chapitre lorsque nécessaire; considérez-le comme un aide-mémoire.

1.1 Importation de données géographiques

Quels packages choisir pour importer et manipuler des données spatiales?

Pour les données vectorielles, il existe deux principaux packages (équivalent d’une librairie dans Python) : sp (Pebesma et Bivand 2005; Bivand, Pebesma et Gomez-Rubio 2013) et sf (Pebesma 2018). Puisque le package sp est progressivement délaissé par R, il est donc fortement conseillé d’utiliser sf.

Pour les données raster, il est possible d’utiliser les packages raster (Hijmans 2022a) et terra (Hijmans 2022b), dont le dernier, plus récent, semblerait plus rapide.

Cette transition de sp à sf et de raster à terra est assez récente et encore en cours durant l’écriture de ce livre. Il existe encore de nombreux packages basés sur sp et raster. Il est donc possible que vous ayez à les utiliser, car leur transition n’est peut-être pas encore effectuée. Notez que la façon dont ces anciens packages intègrent les données vectorielles et matricielles dans R est très différente de celle des nouveaux packages. À titre d’exemple, la fonction sp::readOGR lit un fichier shapefile, tout comme la fonction sf::st_read, mais la première produit un objet de type SpatialDataFrame, alors que la seconde produit un tbl_df. Dans le premier cas, les géométries et les données sont stockées dans deux éléments séparés, alors que dans le second cas, le tbl_df est un data.frame avec une colonne contenant les géométries.

Pour les personnes intéressées aux motivations ayant conduit à cette transition, consultez cet excellent article de blog. Il existe deux raisons principales : le mainteneur des packages rgdal et rgeos servant de fondation à raster et sp a pris sa retraite. À cela s’ajoutent le côté « vieille école » de ces packages (ayant plus de 20 ans!) et l’apparition de packages plus modernes. Il s’agit d’un bon exemple de ce qui peut arriver dans une communauté open source et des évolutions constantes de l’environnement R.

En résumé, privilégiez l’utilisation de sf et de terra.

Il convient d’installer les deux packages. Notez que l’installation d’un package requiert une connexion Internet, car R accède au répertoire de packages CRAN pour télécharger le package et l’installer sur votre ordinateur. Cette opération est réalisée avec la fonction install.packages("nom du package"). Notez qu’une fois que le package est installé, il est enregistré localement sur votre ordinateur et y reste à moins de le désinstaller avec la fonction remove.packages("nom du package").

Autrement dit, il n’est pas nécessaire de les installer à chaque ouverture de R! Pour utiliser les fonctions d’un package, vous devez préalablement le charger avec la fonction library("Nom du package") (équivalent à la fonction import de Python).

Pour plus d’informations sur l’installation et le chargement de packages, consultez la section suivante (Apparicio et Gelb 2022).

1.1.1 Importation de données vectorielles

La fonction st_read de sf permet d’importer une multitude de formats de données géographiques, comme des fichiers shapefile (shp), GeoPackage (GPKG), GeoJSON (geojson), sqlite (sqlite), geodatabase d’ESRI (FileGDB), Geoconcept (gxt), Keyhole Markup Language (kml), Geography Markup Language (gml), etc.

1.1.1.1 Importation d’un fichier shapefile

Le code R ci-dessous permet d’importer des couches géographiques au format shapefile. Notez que la fonction list.files(pattern = ".shp") renvoie préalablement la liste des couches shapefile présentes dans le dossier de travail.

## Chargement des packages
library("sf")
library("terra")
library("tmap")
library("ggplot2")
library("ggpubr")
library("foreign")
library("xlsx")
library("rmapshaper")
library("RColorBrewer")
## Obtention d'une liste des shapefiles dans le dossier de travail
list.files(path = "data/chap01/shp", pattern = ".shp")

 [1] "AbidjanPtsGPS.shp"                         
 [2] "AbidjanSegRue.shp"                         
 [3] "Arrondissements.shp"                       
 [4] "IncidentsSecuritePublique.shp"             
 [5] "Installations_sportives_et_recreatives.shp"
 [6] "Pistes_cyclables.shp"                      
 [7] "PolyX.shp"                                 
 [8] "PolyY.shp"                                 
 [9] "Quebec.shp"                                
[10] "Segments_de_rue.shp"                       

## Importation des shapefiles avec sf
Arrondissements <- st_read("data/chap01/shp/Arrondissements.shp", quiet=TRUE)
InstallationSport <- st_read("data/chap01/shp/Installations_sportives_et_recreatives.shp", quiet=TRUE)
PistesCyclables <- st_read("data/chap01/shp/Pistes_cyclables.shp", quiet=TRUE)
Rues <- st_read("data/chap01/shp/Segments_de_rue.shp", quiet=TRUE)

Regardons à présent la structure des couches importées. Pour ce faire, nous utilisons la fonction head(nom du DataFrame, n=2); notez que le paramètre n permet de spécifier le nombre des premiers enregistrements à afficher. Les informations suivantes sont ainsi disponibles :

• 6 fields : six champs attributaires (TYPE, DETAIL, NOM, SURFACE, ECLAIRAGE, OBJECTID).

• Geometry type POINT : le type de géométrie est point.

• Bounding box: xmin: -8009681 ymin: 5686891 xmax: -8001939 ymax: 5696536 : les quatre coordonnées définissant l’enveloppe de la couche.

• Projected CRS: WGS 84 / Pseudo-Mercator : la projection cartographique. Ici, une projection cartographique utilisée par Google Maps et OpenStreetMap.

• La géométrie est enregistrée dans le champ geometry. Pour le premier enregistrement, nous avons la valeur POINT (-8001939 5686891), soit un point avec les coordonnées géographiques (x,y) entre parenthèses.

head(InstallationSport, n=2)   # Visualisation des deux premiers enregistrements

Simple feature collection with 2 features and 6 fields
Geometry type: POINT
Dimension:     XY
Bounding box:  xmin: -8009681 ymin: 5686891 xmax: -8001939 ymax: 5696536
Projected CRS: WGS 84 / Pseudo-Mercator
   TYPE DETAIL                     NOM SURFACE ECLAIRAGE OBJECTID
1 Aréna   <NA>    Aréna Eugène-Lalonde    <NA>      <NA>        1
2 Aréna   <NA> Aréna Philippe-Bergeron    <NA>      <NA>        2
                  geometry
1 POINT (-8001939 5686891)
2 POINT (-8009681 5696536)

names(InstallationSport)       # Noms de champs (colonnes)

[1] "TYPE"      "DETAIL"    "NOM"       "SURFACE"   "ECLAIRAGE" "OBJECTID" 
[7] "geometry" 

View(InstallationSport)        # Afficher l'ensemble de la table attributaire

Explorons les types de géométries et la projection des autres couches avec le code ci-dessous. En résumé, les types de géométries sont :

• Des géométries simples

  • point : un seul point.

  • linestring : une séquence de deux points et plus formant une ligne.

  • polygon : un seul polygone formé par une séquence de points pouvant contenir un ou plusieurs polygones intérieurs formant des trous.

• Des géométries multiples

  • multipoint : plusieurs points pour une même observation.

  • multilinestring : plusieurs lignes pour une même observation.

  • multipolygon : plusieurs polygones pour une même observation.

• Une collection de géométries (Geometrycollection) qui peut contenir différents types de géométries décrites ci-dessus pour une même observation.

head(PistesCyclables, n=2)

Simple feature collection with 2 features and 3 fields
Geometry type: MULTILINESTRING
Dimension:     XY
Bounding box:  xmin: -8010969 ymin: 5666202 xmax: -7997972 ymax: 5697954
Projected CRS: WGS 84 / Pseudo-Mercator
                       NOM OBJECTID SHAPE__Len                       geometry
1     Axe de la Massawippi        1   13944.09 MULTILINESTRING ((-8010969 ...
2 Axe de la Saint-François        2   19394.28 MULTILINESTRING ((-8001909 ...

head(Rues, n=2)

Simple feature collection with 2 features and 16 fields
Geometry type: MULTILINESTRING
Dimension:     XY
Bounding box:  xmin: -8013896 ymin: 5681299 xmax: -8008810 ymax: 5695980
Projected CRS: WGS 84 / Pseudo-Mercator
  ID         TOPONYMIE NOROUTE NUMEROCIVI NUMEROCI_1 NUMEROCI_2 NUMEROCI_3
1  1 Rue Oliva-Turgeon      NA          0          0          0          0
2  9      Rue Melville      NA          0          0          0          0
     NOMGENERIQ TYPERUE TYPESEGMEN VITESSE         TYPESENSUN MUNICIPALI
1 OLIVA-TURGEON     Rue     Locale      50 Pas de sens unique      43027
2      MELVILLE     Rue     Locale      50 Pas de sens unique      43027
  OBJECTID SHAPE__Len              CIRCULATIO                       geometry
1        1   114.7781 Interdite en tout temps MULTILINESTRING ((-8008810 ...
2        2   114.4441 Interdite en tout temps MULTILINESTRING ((-8013782 ...

head(Arrondissements, n=2)

Simple feature collection with 2 features and 2 fields
Geometry type: POLYGON
Dimension:     XY
Bounding box:  xmin: -8027109 ymin: 5668860 xmax: -8000502 ymax: 5704391
Projected CRS: WGS 84 / Pseudo-Mercator
  NUMERO                                                         NOM
1      1 Arrondissement de Brompton–Rock Forest–Saint-Élie–Deauville
2      4                                  Arrondissement des Nations
                        geometry
1 POLYGON ((-8005013 5702777,...
2 POLYGON ((-8005680 5690860,...

Visualisons quelques couches importées avec ggplot().

## Arrondissements et rues
ggplot()+ geom_sf(data = Arrondissements, lwd = .8)+
  geom_sf(data = Rues, aes(colour = TYPESEGMEN))

## Arrondissements, pistes cyclables et installations sportives
ggplot()+ geom_sf(data = Arrondissements, lwd = .8)+
  geom_sf(data = PistesCyclables, aes(colour = NOM), lwd = .5)+
  geom_sf(data = InstallationSport)

1.1.1.2 Importation d’une couche dans un GeoPackage

Pour importer une couche stockée dans un GeoPackage (GPKG), vous devez spécifier le fichier et la couche avec respectivement les paramètres dsn et layer de la fonction st_read. Le code ci-dessous permet d’importer les secteurs de recensement de la région métropolitaine de recensement de Sherbrooke pour l’année 2021. Notez que la fonction st_layers(dsn) permet d’obtenir la liste des couches contenues dans le fichier GPKG, avec le type de géométrie, les nombre d’entités spatiales et de champs, et la projection cartographique pour chacune d’elles.

## Nom du fichier GPKG
fichierGPKG <- "data/chap01/gpkg/Recen2021Sherbrooke.gpkg"
## Liste des couches dans le GPKG
st_layers(dsn=fichierGPKG, do_count = TRUE)

Driver: GPKG 
Available layers:
           layer_name geometry_type features fields
1            SherbRMR Multi Polygon        1     12
2            SherbSDR Multi Polygon       11     12
3             SherbSR Multi Polygon       50     10
4             SherbAD Multi Polygon      333     10
5             SherbIL Multi Polygon     2734     12
6        RegionEstrie Multi Polygon        1      5
7          sdr_Estrie Multi Polygon       89      6
8        DREstrie2021 Multi Polygon        7      6
9 DivisionsRecens2021 Multi Polygon       98      6
                           crs_name
1 NAD83 / Statistics Canada Lambert
2 NAD83 / Statistics Canada Lambert
3 NAD83 / Statistics Canada Lambert
4 NAD83 / Statistics Canada Lambert
5 NAD83 / Statistics Canada Lambert
6 NAD83 / Statistics Canada Lambert
7 NAD83 / Statistics Canada Lambert
8 NAD83 / Statistics Canada Lambert
9 NAD83 / Statistics Canada Lambert

## Importation d'une couche
SR.RMRSherb <- st_read(dsn = fichierGPKG, 
                       layer = "SherbSR", quiet=TRUE)
## Affichage des deux premiers enregistrements
head(SR.RMRSherb, n=2)

Simple feature collection with 2 features and 10 fields
Geometry type: MULTIPOLYGON
Dimension:     XY
Bounding box:  xmin: 7762066 ymin: 1271201 xmax: 7765357 ymax: 1274082
Projected CRS: NAD83 / Statistics Canada Lambert
                IDUGD      SRIDU   SRNOM SUPTERRE PRIDU SRpop_2021 SRtlog_2021
1 2021S05074330001.00 4330001.00 0001.00   3.1882    24       5637        2918
2 2021S05074330002.00 4330002.00 0002.00   0.8727    24       1868        1169
  SRrhlog_2021 RMRcode   HabKm2                           geom
1         2756     433 1768.082 MULTIPOLYGON (((7764998 127...
2         1063     433 2140.484 MULTIPOLYGON (((7763361 127...

## Visualisation rapide des secteurs avec ggplot
ggplot()+ geom_sf(data = SR.RMRSherb, lwd = .5)

1.1.1.3 Importation d’une couche dans une geodatabase d’ESRI

La logique est la même qu’avec un GeoPackage, nous spécifions le chemin de la geodatabase et la couche avec les paramètres dsn et layer.

AffectDuTerritoire <- st_read(dsn = "data/chap01/geodatabase/Sherbrooke.gdb", 
                              layer = "AffectationsDuTerritoire", quiet=TRUE)
## Visualisation des affectations du sol avec ggplot
ggplot()+ geom_sf(data = AffectDuTerritoire, aes(fill = TYPE), lwd = .2)

1.1.1.4 Importation de données GPS

En géomatique appliquée, il est fréquent de collecter des données sur le terrain avec un appareil GPS. Les données ainsi collectées peuvent être enregistrées dans différents formats de données dépendamment de l’appareil GPS utilisé : GPS eXchange Format (GPX), Garmin’s Flexible and Interoperable Data Transfer (FIT), Training Center XML (TCX), etc.

1.1.1.4.1 Importation de coordonnées GPS longitude/latitude au format csv

Une personne ayant collecté des données sur le terrain pourrait aussi vous les transmettre dans un fichier csv (fichier texte délimité par des virgules). Il convient d’importer le fichier de coordonnées GPS dans R dans un DataFrame (avec la fonction read.csv). Une fois importé, nous constatons qu’il comprend trois champs :

• id : un champ identifiant avec des valeurs uniques.

• lon : longitude.

• lat : latitude.

Les points sont projetés en longitude/latitude (WGS84 long/lat, EPSG : 4326).

## Importation du fichier csv
PointsGPS <- read.csv("data/chap01/gps/pointsGPS.csv")
head(PointsGPS)

  id       lon      lat
1  1 -71.99985 45.36010
2  2 -71.99096 45.37535
3  3 -71.98444 45.46964
4  4 -72.09873 45.37126
5  5 -72.04880 45.41035
6  6 -71.95000 45.32570

Pour convertir le DataFrame en un objet sf, nous utilisons la fonction st_as_sf en spécifiant les champs pour les coordonnées et la projection cartographique.

## Importation du fichier csv
PointsGPS <- st_as_sf(PointsGPS, coords = c("lon","lat"), crs = 4326)

Les points ainsi créés sont localisés dans la ville de Sherbrooke.

## Affichage des points avec le package tmap
tmap_mode("view") ## Mode actif de tmap
tm_shape(PointsGPS)+
  tm_dots(size = 0.05, shape = 21, col = "red")

1.1.1.4.2 Importation de coordonnées GPS au format GPX

Le format GPX est certainement le format de stockage et d’échange de coordonnées GPS le plus utilisé. Les informations géographiques (x,y) et temporelles (date et heure) sont respectivement enregistrées en degrés longitude/latitude (projection WSG) (WGS84, EPSG : 4326) et en temps universel coordonné (UTC, format ISO 8601).

Pour importer un fichier GPX, nous utilisons le package gpx. S’il n’est pas installé sur votre ordinateur, lancez la commande install.packages("gpx") dans la console de R; n’oubliez pas de le charger avec library("gpx")! Ensuite, importez le fichier GPX avec la fonction read_gpx, enregistrez la trace GPS dans un DataFrame et convertissez-la en objet sf.

library("gpx")
## Importation du fichier GPX
TraceGPS <- read_gpx("data/chap01/gps/TraceGPS.gpx")
## Cette trace GPS comprend trois listes : routes, tracks et waypoints
## Les points sont stockés dans tracks
names(TraceGPS)

[1] "routes"    "tracks"    "waypoints"

## Pour visualiser les données, il suffit de lancer la ligne
## ci-dessous (mise en commentaire car le résultat est un peu long...)
# head(TraceGPS)
TraceGPS <- TraceGPS$tracks$`ID1_PA_2021-12-03_TRAJET01.gpx`
## Conversion du DataFrame en objet sf
TraceGPS <- st_as_sf(TraceGPS, coords = c("Longitude","Latitude"), crs = 4326)
## Visualisation des premiers enregistrements
head(TraceGPS, n=2)

Simple feature collection with 2 features and 4 fields
Geometry type: POINT
Dimension:     XY
Bounding box:  xmin: -4.022827 ymin: 5.327383 xmax: -4.022825 ymax: 5.327387
Geodetic CRS:  WGS 84
  Elevation                Time extensions Segment ID
1      40.8 2021-12-03 08:38:49         NA          1
2      40.6 2021-12-03 08:38:50         NA          1
                    geometry
1 POINT (-4.022827 5.327387)
2 POINT (-4.022825 5.327383)

La trace GPS correspond à un trajet réalisé à vélo à Abidjan (Côte d’Ivoire) le 3 décembre 2021. Cette trace a été obtenue avec une montre Garmin et comprend un point chaque seconde.

tmap_mode("view")
tm_basemap(leaflet::providers$OpenStreetMap)+
tm_shape(TraceGPS)+
  tm_dots(size = 0.001, shape = 21, col = "red")

La structure de la classe sf

La classe sf est composée de trois éléments (figure 1.1) :

• L’objet simple feature geometry (sfg) est la géométrie d’une observation. Tel que vu plus haut, elle est une géométrie simple (point, linestring, polygon), multiple (multipoint, multilinestring, multipolygon) ou une collection de géométries différentes (Geometrycollection). Pour définir chacune de ces géométries, nous utilisons les méthodes st_point(), st_linestring(), st_polygon(), st_multipoint(), st_multilinestring(), st_multipolygon() et Geometrycollection().

• L’objet simple feature column (sfc) est simplement une liste de simple feature geometry (sfg). Elle représente la colonne geometry d’une couche vectorielle sf.

• L’objet data.frame correspond à la table attributaire.

Une simple feature correspond ainsi à une observation (ligne) d’un objet sf, soit une entité spatiale comprenant l’information sémantique (attributs) et l’information spatiale (géométrie).

Figure 1.1: Structure de la classe sf

Voyons un exemple concret : créons une couche sf comprenant les trois entités spatiales décrites dans la figure 1.1.

## Création des géométries : simple feature geometry (sfg)
point1 = st_point(c(-8001939, 5686891))
point2 = st_point(c(-8009681, 5696536))
point3 = st_point(c(-7998695, 5689743))
## Création d'une liste de géométries : simple feature geometry (sfc)
## avec la projection cartographique EPSG 3857
points_sfc = st_sfc(point1, point2, point3, crs = 3857)
## Création de la table attributaire : objet data.frame
table_attr = data.frame(TYPE = c("Aréna", "Aréna","Aréna"),
                       NOM = c("Aréna Eugène-Lalonde", 
                               "Aréna Philippe-Bergeron",
                               "Centre Julien-Ducharme"),
                       OBJECTID = c(1, 2, 3))
## Création de l'objet sf
Arena_sf = st_sf(table_attr, geometry = points_sfc)
## Le résultat est bien identique à celui de la figure ci-dessus
head(Arena_sf)

Simple feature collection with 3 features and 3 fields
Geometry type: POINT
Dimension:     XY
Bounding box:  xmin: -8009681 ymin: 5686891 xmax: -7998695 ymax: 5696536
Projected CRS: WGS 84 / Pseudo-Mercator
   TYPE                     NOM OBJECTID                 geometry
1 Aréna    Aréna Eugène-Lalonde        1 POINT (-8001939 5686891)
2 Aréna Aréna Philippe-Bergeron        2 POINT (-8009681 5696536)
3 Aréna  Centre Julien-Ducharme        3 POINT (-7998695 5689743)

1.1.2 Importation de données raster

La fonction terra::rast permet d’importer des images de différents formats (GeoTiff, ESRI, ENVI, ERDAS, BIN, GRID, etc.). Nous importons ci-dessous cinq feuillets de modèles numériques d’altitude (MNA) à l’échelle du 1/20000 couvrant la ville de Sherbrooke. La figure 1.2 présente l’un d’entre eux.

## Liste des fichiers GeoTIFF dans le dossier
list.files(path="data/chap01/raster", pattern = ".tif")

 [1] "f21e05_101.tif"         "f21e05_101.tif.aux.xml" "f21e05_201.tif"        
 [4] "f21e05_201.tif.aux.xml" "f21e12_101.tif"         "f21e12_101.tif.aux.xml"
 [7] "f31h08_102.tif"         "f31h08_102.tif.aux.xml" "f31h08_202.tif"        
[10] "f31h08_202.tif.aux.xml"

## Importation des fichiers
f21e05_101 <- terra::rast("data/chap01/raster/f21e05_101.tif")
f21e05_201 <- terra::rast("data/chap01/raster/f21e05_201.tif")
f31h08_102 <- terra::rast("data/chap01/raster/f31h08_102.tif")
f31h08_202 <- terra::rast("data/chap01/raster/f31h08_202.tif")
f21e12_101 <- terra::rast("data/chap01/raster/f21e12_101.tif")
## Visualisation des informations sur l'image f21e05_101
f21e05_101

class       : SpatRaster 
dimensions  : 1409, 2798, 1  (nrow, ncol, nlyr)
resolution  : 9e-05, 9e-05  (x, y)
extent      : -72.00095, -71.74913, 45.24907, 45.37588  (xmin, xmax, ymin, ymax)
coord. ref. : lon/lat NAD83 (EPSG:4269) 
source      : f21e05_101.tif 
name        : f21e05_101 
min value   :   143.4273 
max value   :   423.5806 

# Visualisation de l'image
terra::plot(f21e05_101, 
     main="Modèle numérique d'altitude à l’échelle de 1/20 000 (f21e05_101)")

Figure 1.2: Modèle numérique d’élévation au 1/20000 (feuillet f21e05_101)

1.2 Manipulation de données vectorielles

Package sf et opérations géométriques

Le package sf est une librairie extrêmement complète permettant de réaliser une multitude d’opérations géométriques sur des couches vectorielles comme dans un système d’information géographique (SIG). Notre objectif n’est pas de toutes les décrire, mais d’aborder les principales. Au fil de vos projets avec sf, vous apprendrez d’autres fonctions. Pour ce faire, n’hésitez pas à consulter :

• Une belle Cheatsheet sur sf. Allez y jeter un œil, cela vaut la peine!

• Sur le site CRAN de sf, vous trouverez plusieurs vignettes explicatives (exemples de code documentés).

• La documentation complète en PDF.

La syntaxe methods(class = 'sfc') renvoie la liste des méthodes implémentées dans le package sf. Pour accéder à l’aide en ligne de l’une d’entre elles, écrivez simplement ?Nom de la fonction (ex. : ?st_buffer).

methods(class = 'sfc')

 [1] [                            [<-                         
 [3] as.data.frame                c                           
 [5] coerce                       format                      
 [7] fortify                      identify                    
 [9] initialize                   ms_clip                     
[11] ms_dissolve                  ms_erase                    
[13] ms_explode                   ms_filter_islands           
[15] ms_innerlines                ms_lines                    
[17] ms_points                    ms_simplify                 
[19] Ops                          print                       
[21] rep                          scale_type                  
[23] show                         slotsFromS3                 
[25] st_area                      st_as_binary                
[27] st_as_grob                   st_as_s2                    
[29] st_as_sf                     st_as_text                  
[31] st_bbox                      st_boundary                 
[33] st_break_antimeridian        st_buffer                   
[35] st_cast                      st_centroid                 
[37] st_collection_extract        st_concave_hull             
[39] st_convex_hull               st_coordinates              
[41] st_crop                      st_crs                      
[43] st_crs<-                     st_difference               
[45] st_geometry                  st_inscribed_circle         
[47] st_intersection              st_intersects               
[49] st_is                        st_is_valid                 
[51] st_line_merge                st_m_range                  
[53] st_make_valid                st_minimum_rotated_rectangle
[55] st_nearest_points            st_node                     
[57] st_normalize                 st_point_on_surface         
[59] st_polygonize                st_precision                
[61] st_reverse                   st_sample                   
[63] st_segmentize                st_set_precision            
[65] st_shift_longitude           st_simplify                 
[67] st_snap                      st_sym_difference           
[69] st_transform                 st_triangulate              
[71] st_triangulate_constrained   st_union                    
[73] st_voronoi                   st_wrap_dateline            
[75] st_write                     st_z_range                  
[77] st_zm                        str                         
[79] summary                      vec_cast.sfc                
[81] vec_ptype2.sfc               vect                        
see '?methods' for accessing help and source code

1.2.1 Fonctions relatives à la projection cartographique

Les trois principales fonctions relatives à la projection cartographique des couches vectorielles sont :

• st_crs(x) pour connaître la projection géographique d’un objet sf.

• st_transform(x, cr) pour modifier la projection cartographique.

• st_is_longlat(x) pour vérifier si les coordonnées sont en degrés longitude/latitude.

## Importation d'un shapefile pour la province de Québec
ProvinceQc <- st_read("data/chap01/shp/Quebec.shp", quiet = TRUE)
## La projection est EPSG:3347 - NAD83 / Statistics Canada Lambert,
## soit la projection conique conforme de Lambert
st_crs(ProvinceQc)

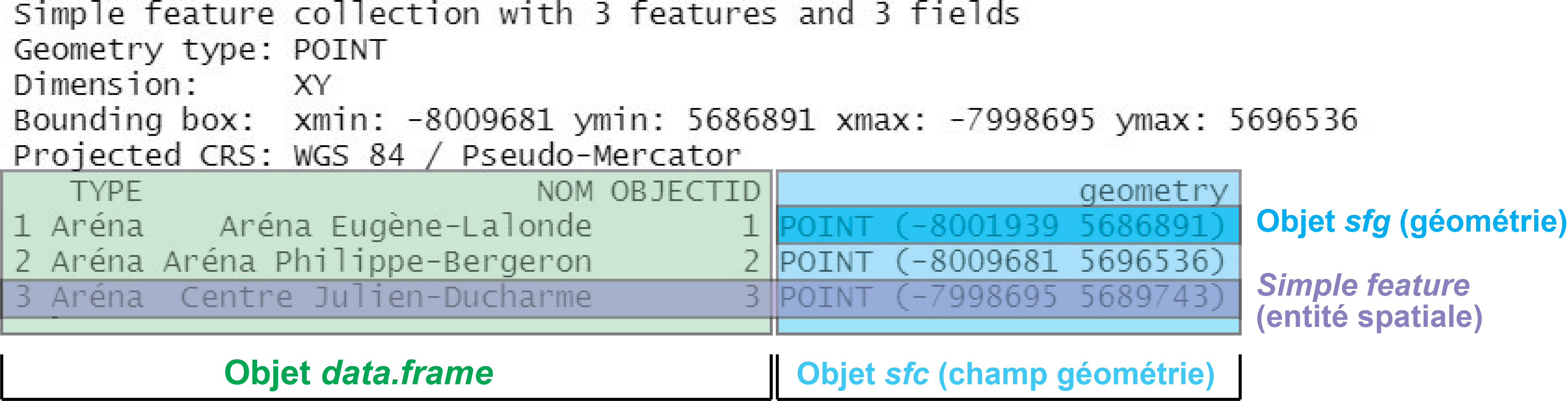
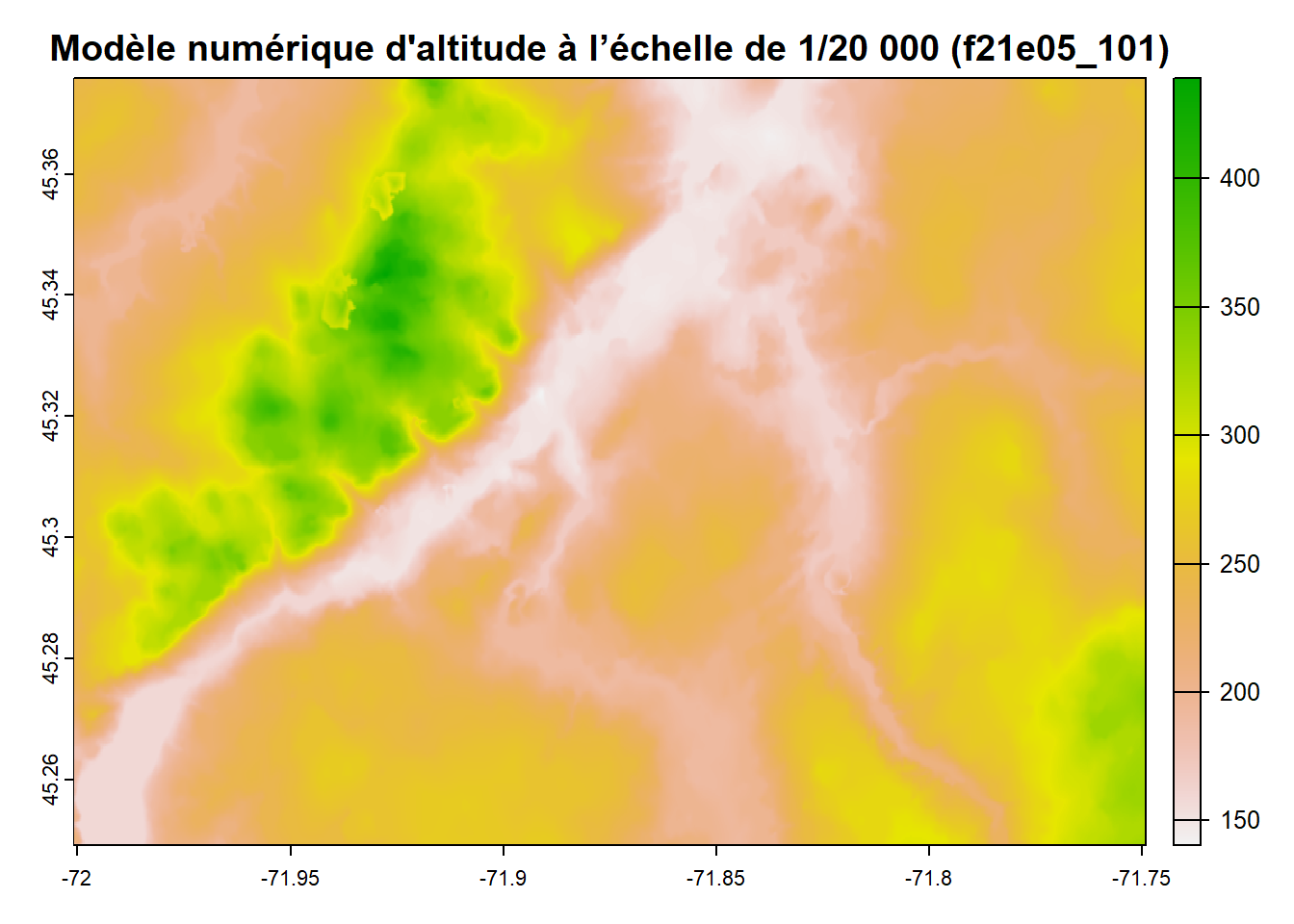
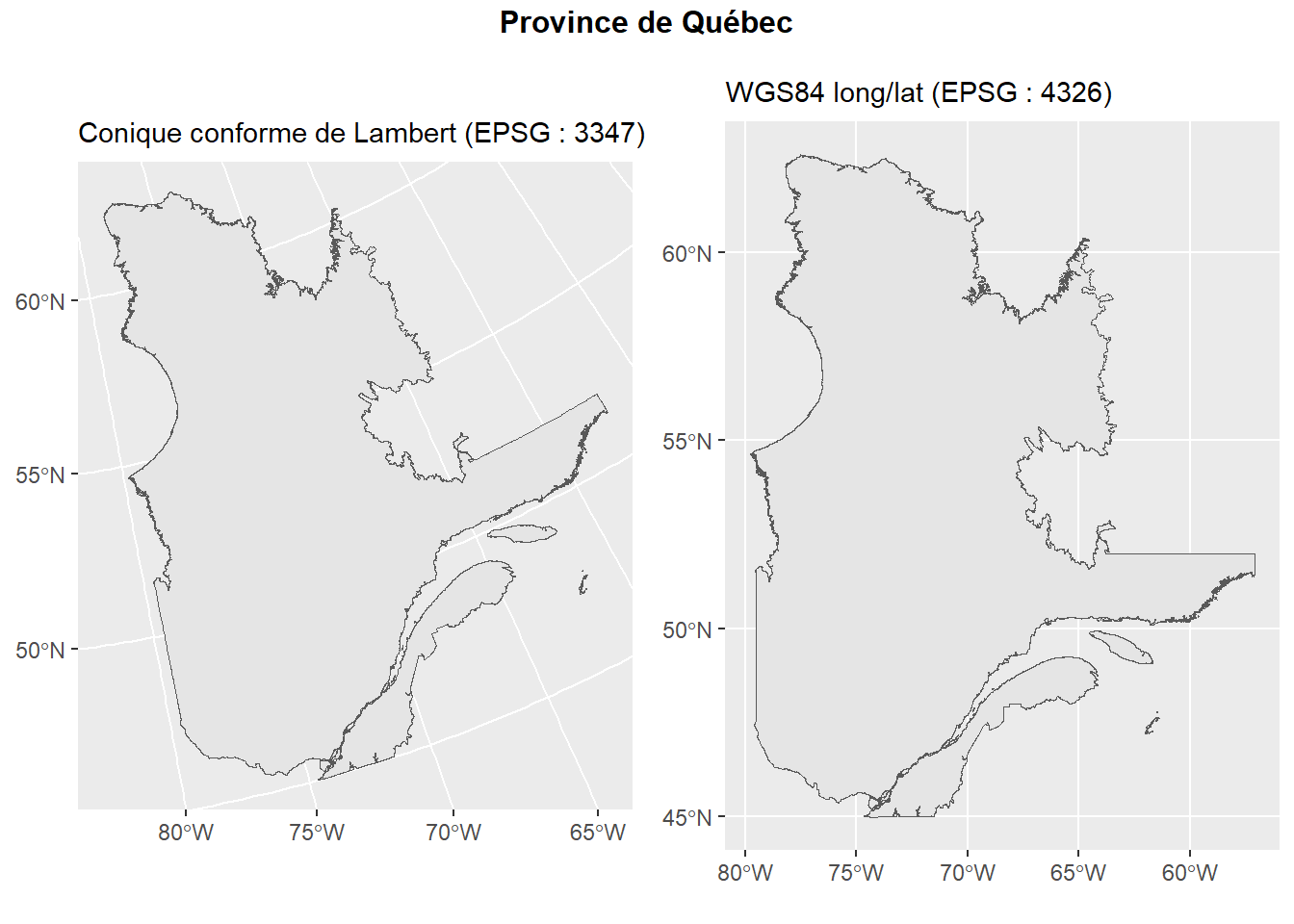
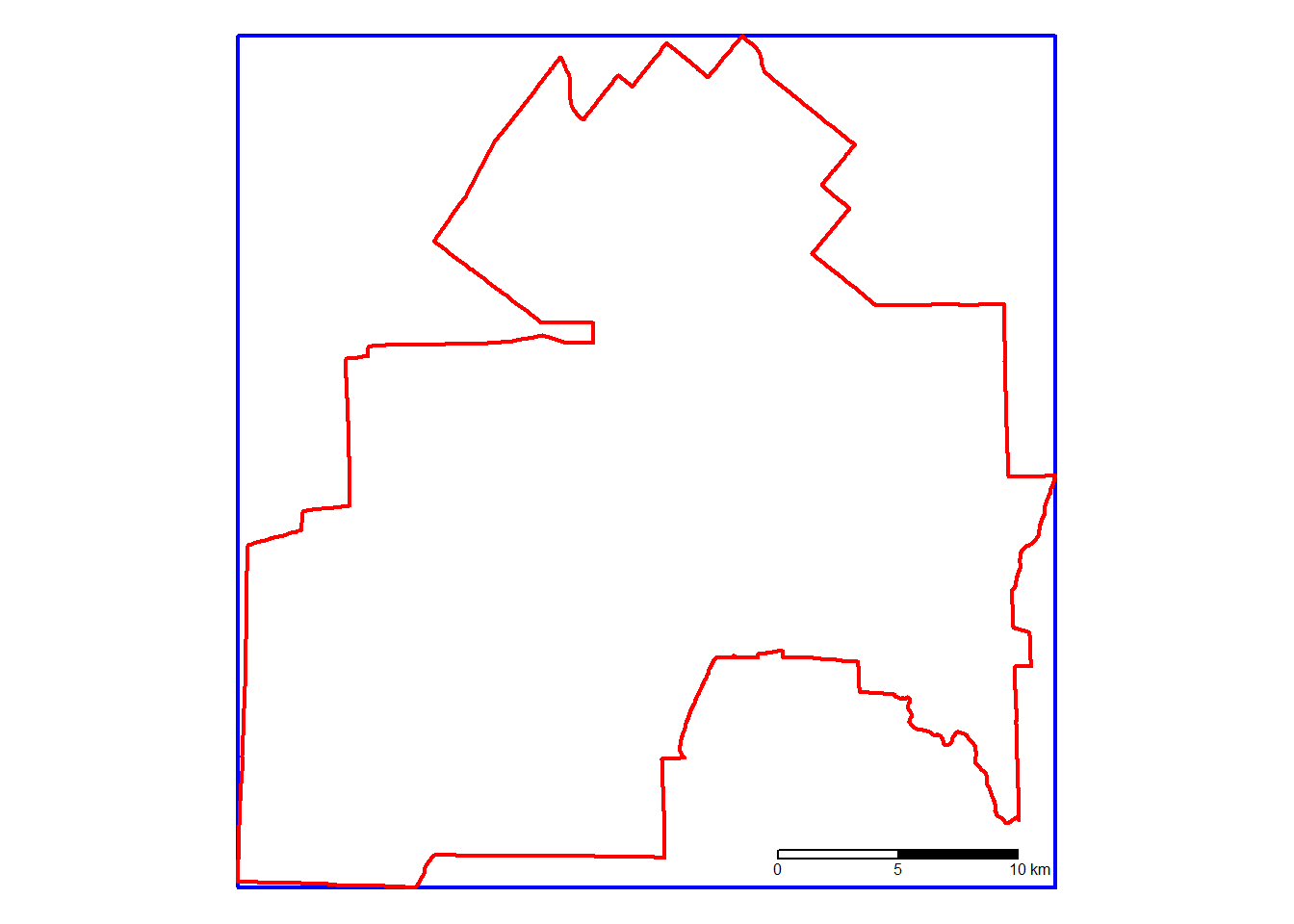
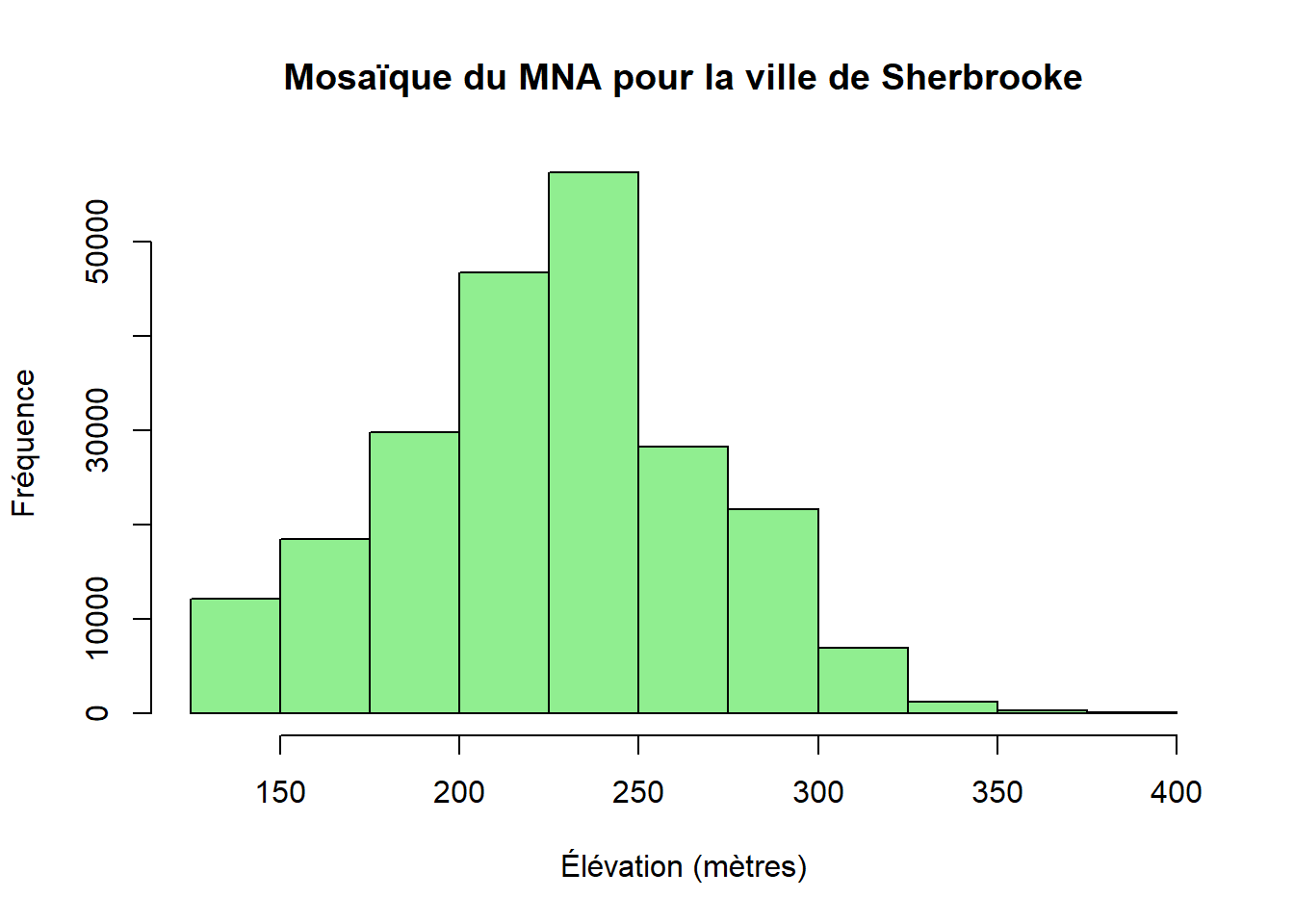
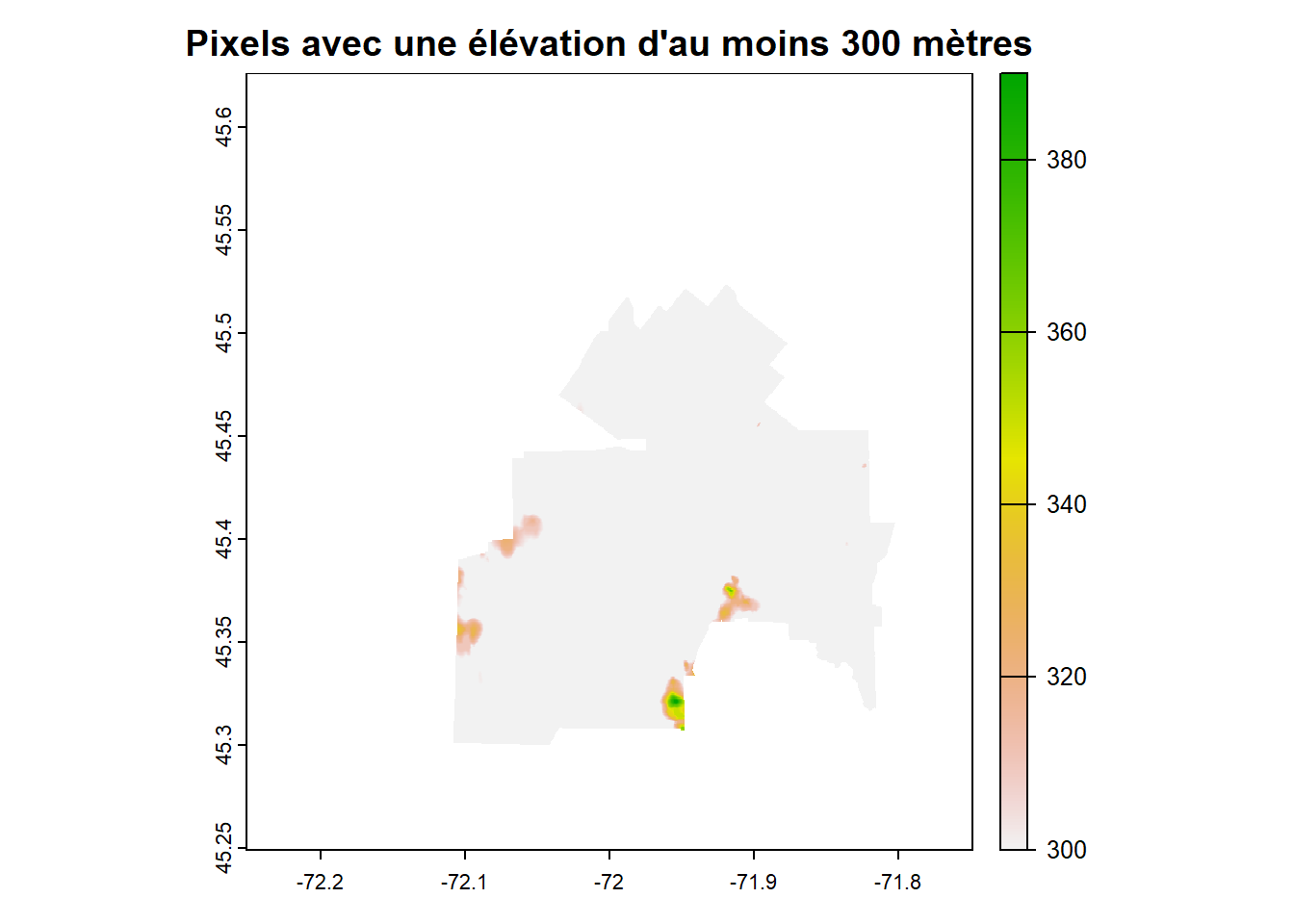
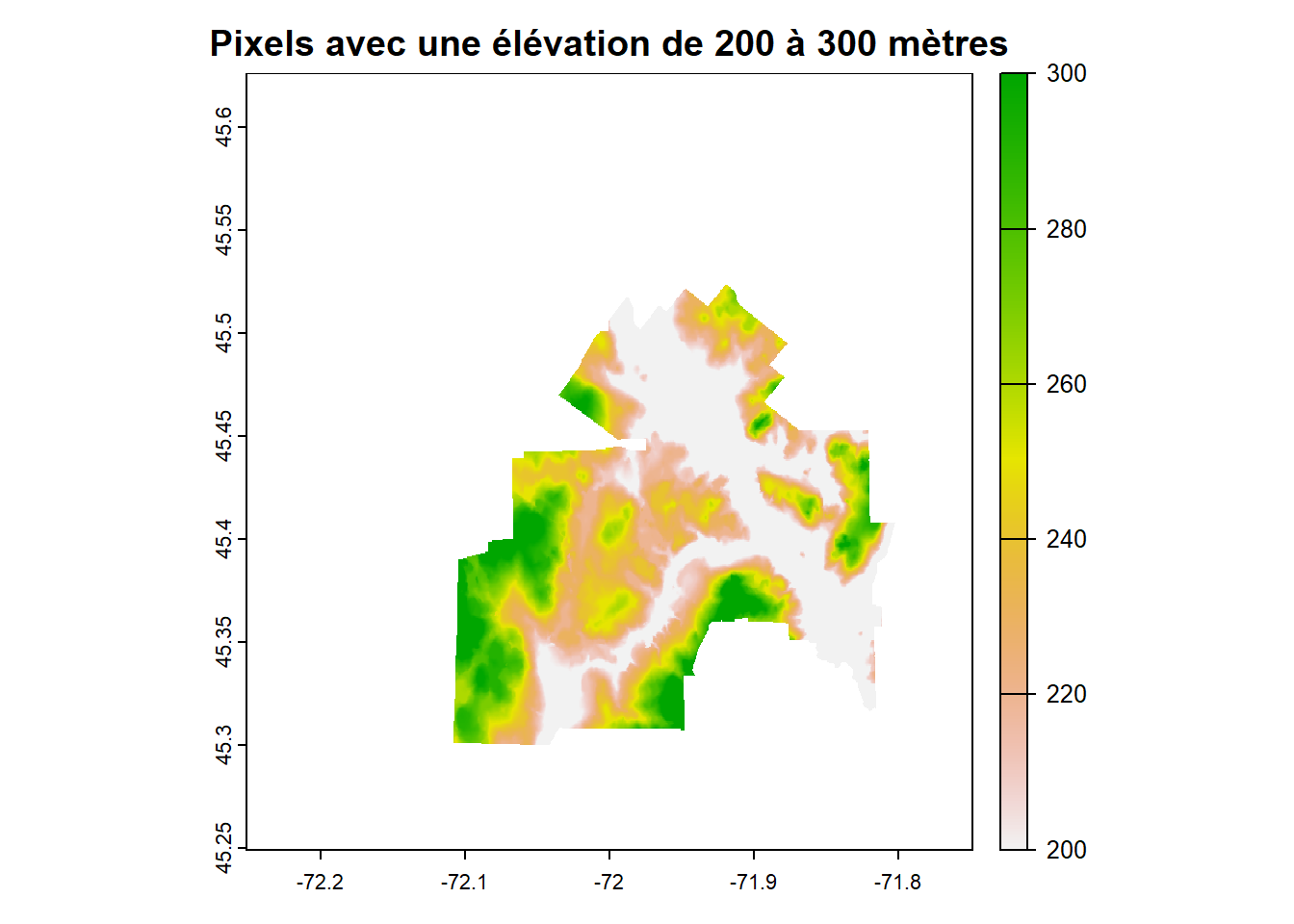
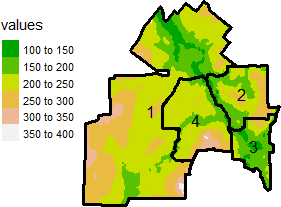
Coordinate Reference System:
  User input: NAD83 / Statistics Canada Lambert 
  wkt:
PROJCRS["NAD83 / Statistics Canada Lambert",
    BASEGEOGCRS["NAD83",
        DATUM["North American Datum 1983",
            ELLIPSOID["GRS 1980",6378137,298.257222101,
                LENGTHUNIT["metre",1]]],
        PRIMEM["Greenwich",0,
            ANGLEUNIT["degree",0.0174532925199433]],
        ID["EPSG",4269]],
    CONVERSION["Statistics Canada Lambert",
        METHOD["Lambert Conic Conformal (2SP)",
            ID["EPSG",9802]],
        PARAMETER["Latitude of false origin",63.390675,
            ANGLEUNIT["degree",0.0174532925199433],
            ID["EPSG",8821]],
        PARAMETER["Longitude of false origin",-91.8666666666667,
            ANGLEUNIT["degree",0.0174532925199433],
            ID["EPSG",8822]],
        PARAMETER["Latitude of 1st standard parallel",49,
            ANGLEUNIT["degree",0.0174532925199433],
            ID["EPSG",8823]],
        PARAMETER["Latitude of 2nd standard parallel",77,
            ANGLEUNIT["degree",0.0174532925199433],
            ID["EPSG",8824]],
        PARAMETER["Easting at false origin",6200000,
            LENGTHUNIT["metre",1],
            ID["EPSG",8826]],
        PARAMETER["Northing at false origin",3000000,
            LENGTHUNIT["metre",1],
            ID["EPSG",8827]]],
    CS[Cartesian,2],
        AXIS["(E)",east,
            ORDER[1],
            LENGTHUNIT["metre",1]],
        AXIS["(N)",north,
            ORDER[2],
            LENGTHUNIT["metre",1]],
    USAGE[
        SCOPE["Topographic mapping (small scale)."],
        AREA["Canada - onshore and offshore - Alberta; British Columbia; Manitoba; New Brunswick; Newfoundland and Labrador; Northwest Territories; Nova Scotia; Nunavut; Ontario; Prince Edward Island; Quebec; Saskatchewan; Yukon."],
        BBOX[38.21,-141.01,86.46,-40.73]],
    ID["EPSG",3347]]

## Reprojection de la couche en WGS84 long/lat (EPSG:4326)
ProvinceQc.4326 <- st_transform(ProvinceQc, crs = 4326)
## longitude/latitude?
st_is_longlat(ProvinceQc)

[1] FALSE

st_is_longlat(ProvinceQc.4326)

[1] TRUE

La figure 1.3 démontre bien que les deux couches sont projetées différemment.

Map1 <- ggplot()+geom_sf(data = ProvinceQc)+coord_sf(crs = st_crs(ProvinceQc))+
        labs(subtitle = "Conique conforme de Lambert (EPSG : 3347)")

Map2 <- ggplot()+geom_sf(data = ProvinceQc.4326)+coord_sf(crs = st_crs(ProvinceQc.4326))+
        labs(subtitle = "WGS84 long/lat (EPSG : 4326)")

comp_plot <- ggarrange(Map1, Map2, ncol = 2, nrow = 1)
annotate_figure(comp_plot,
                top = text_grob("Province de Québec",
                                face = "bold", size = 12, just = "center")
                )

Figure 1.3: Deux projections cartographiques

1.2.2 Fonctions d’opérations géométriques sur une couche

Il existe une quinzaine de fonctions d’opérations géométriques sur une couche dans le package sf dont le résultat renvoie de nouvelles géométries (voir la documentation suivante). Nous décrivons ici uniquement celles qui nous semblent les plus utilisées :

• st_bbox(x) renvoie les coordonnées minimales et maximales des géométries d’un objet sf. Pour créer l’enveloppe d’un objet sf, il suffit donc d’écrire st_as_sfc(st_bbox(x)).

• st_boundary(x) renvoie les limites (contours) des géométries d’un objet sf.

• st_convex_hull(x) crée l’enveloppe convexe des géométries d’un objet sf.

• st_combine(x) regroupe les géométries d’un objet sf en une seule géométrie, sans les réunir ni résoudre les limites internes.

• st_union(x) fusionne les géométries d’un objet sf en une seule géométrie.

• st_buffer(x, dist, endCapStyle = c("ROUND", "FLAT", "SQUARE"), joinStyle = c("ROUND", "MITRE", "BEVEL")) crée des zones tampons d’une distance définie avec le paramètre dist. Cette fonction s’applique à des points, à des lignes et à des polygones.

• st_centroid(x) crée des points au centre de chaque géométrie d’un objet sf. Elle s’applique donc à des lignes et à des polygones.

• st_point_on_surface(x) crée un point au centre de chaque polygone d’un objet sf .

• st_simplify(x, dTolerance) simplifie les contours de géométries (lignes ou polygones) avec une tolérance exprimée en mètres (paramètre dTolerance) d’un objet sf .

• st_voronoi(x, bOnlyEdges = TRUE) crée des polygones de Thiessen, appelés aussi polygones de Voronoï pour des points. Attention, le paramètre bOnlyEdges = TRUE renvoie des lignes tandis que bOnlyEdges = FALSE renvoie des polygones.

1.2.2.1 Enveloppe et union d’une couche

Le code ci-dessous crée une enveloppe (en bleu) et un polygone fusionné (en rouge) pour les arrondissements de la ville de Sherbrooke (figure 1.4). La couche résultante de l’opération st_as_sfc(st_bbox(x)) est ainsi l’équivalent des outils Emprise de QGIS et Minimum Bounding Geometry (Geometry Type = Envelope) d’ArcGIS Pro.

## Enveloppe sur les arrondissements de la ville de Sherbrooke
Arrond.Enveloppe <- st_as_sfc(st_bbox(Arrondissements))
## Fusionne les géométries en une seule en résolvant les limites internes
Arrond.Union <- st_union(Arrondissements)

tmap_mode("plot")
tm_shape(Arrond.Enveloppe) + tm_borders(col = "blue", lwd=2)+
  tm_shape(Arrond.Union) + tm_borders(col = "red", lwd=2)+
  tm_layout(frame = FALSE)+
  tm_scale_bar(c(0,5,10))

Figure 1.4: Enveloppe sur une couche

1.2.2.2 Enveloppe orientée

La fonction st_bbox de sf produit des rectangles englobant des géométries qui sont orientées nord-sud. Il est possible de générer des rectangles orientés autour de géométries pour minimiser leur emprise et ainsi mieux représenter l’orientation de la géométrie initiale. Il n’existe pas de fonction dans sf pour le faire, mais le package foot offre une implémentation facile d’utilisation. Notez que foot n’est pas déposé sur CRAN et doit être téléchargé depuis Github avec la ligne de code ci-dessous.

devtools::install_github("wpgp/foot", build_vignettes = FALSE)

La couche résultante de l’opération fs_mbr(x, returnShape = TRUE) (figure 1.5, b) est ainsi l’équivalent des outils Emprise orientée minimale (OMBB) de QGIS et Minimum Bounding Geometry (Geometry Type = Rectangle by area) d’ArcGIS Pro.

library(foot)
## Rectangles (enveloppes) orientés 
rectangles_oriented <- fs_mbr(Arrondissements, returnShape = TRUE)
rectangles_oriented <- st_as_sf(rectangles_oriented,
                                crs = st_crs(Arrondissements))
rectangles_oriented$NOM <- Arrondissements$NOM
## Rectangles non orientés (nord-sud)
st_bbox_by_feature = function(x) {
  x = st_geometry(x)
  f <- function(y) st_as_sfc(st_bbox(y))
  do.call("c", lapply(x, f))
}
rectangles <- st_as_sf(st_bbox_by_feature(Arrondissements),
                       crs = st_crs(Arrondissements))
rectangles$NOM <- Arrondissements$NOM

Figure 1.5: Enveloppes classiques et orientées

1.2.2.3 Centroïdes et centre de surface

Le code ci-dessous extrait les centres géométriques, c’est-à-dire les centroïdes (en bleu) et les points à l’intérieur des polygones (en rouge) pour les arrondissements de la ville de Sherbrooke (figure 1.6). Ces deux opérations correspondent aux outils centroïdes et Point dans la surface de QGIS et Feature to Point (avec l'option Inside) d’ArcGIS Pro.

## Centroïdes et points dans les polygones sur les arrondissements
Arrond.centroide <- st_centroid(Arrondissements)
Arrond.pointpoly <- st_point_on_surface(Arrondissements)

Figure 1.6: Centroïdes et points à l’intérieur des polygones

1.2.2.4 Zone tampon (buffer)

Une simple ligne de code permet de créer des zones tampons (équivalent des outils Analyse vectorielle/Tampon dans QGIS et Buffer dans ArcGIS Pro). Une fois les zones créées, utilisez la fonction st_union pour fusionner les tampons en un polygone (figure 1.7).

## Zones tampons de 1000 mètres autour des installations sportives et récréatives
InstSports.buffer <- st_buffer(InstallationSport, dist = 1000)
## Si vous souhaitez fusionner les zones tampons, utilisez la fonction st_union
InstSports.bufferUnion <- st_union(InstSports.buffer)
## Zones tampons de 500 mètres autour des lignes
PistesCyclables.buffer <- st_buffer(PistesCyclables, dist = 500)
PistesCyclables.bufferUnion <- st_union(PistesCyclables.buffer)

Figure 1.7: Zones tampons

Notez que pour des polygones, il est possible de créer des polygones intérieurs comme suit : st_buffer(x, dist = - Valeur). Par exemple, le code ci-dessous crée des polygones de 200 mètres autour et à l’intérieur du parc du Mont-Bellevue de la ville de Sherbrooke (figure 1.8).

## Importation de la couche des aires aménagées de la ville de Sherbrooke
AiresAmenag <- st_read(dsn = "data/chap01/geodatabase/Sherbrooke.gdb",
                       layer = "AiresAmenagees", quiet = TRUE)
## Sélection du parc du Mont-Bellevue
MontBellevue <- subset(AiresAmenag, NOM == "Parc du Mont-Bellevue")
## Création d'une zone tampon autour du parc
MontBellevue.ZTA500 <- st_buffer(MontBellevue, dist = 200)
## Création d'une zone tampon à l'intérieur du parc
MontBellevue.ZTI500 <- st_buffer(MontBellevue, dist = -200)

Figure 1.8: Zone tampon intérieure et zone tampon extérieure

1.2.2.5 Simplification de géométries

La simplification ou généralisation d’une couche de lignes ou de polygones permet de supprimer des sommets tout en gardant le même nombre de géométries dans la couche résultante. Cette opération peut être réalisée dans QGIS avec l’outil simplifier et dans ArcGIS Pro avec l’outil Generalize. Deux raisons principales peuvent motiver le recours à cette opération :

• La réduction de la taille du fichier, surtout si la couche est utilisée pour de la cartographie interactive sur Internet avec des formats vectoriels comme le SVG (Scalable Vector Graphics), le KML ou le GeoJSON.

• L’utilisation de la couche à une plus petite échelle cartographique nécessitant la suppression de détails.

Le code suivant permet de simplifier les contours des arrondissements de la ville de Sherbrooke avec des tolérances de 250, 500, 1000 et 2000 mètres. Plus la valeur de la tolérance est élevée, plus les contours sont simplifiés (figure 1.9). Notez que l’algorithme de Douglas-Peucker (Douglas et Peucker 1973) a été implémenté dans la fonction st_simplify. Bien qu’intéressant, cet algorithme ne conserve pas les frontières entre les polygones.

## Simplification des contours avec différentes distances de tolérance
Arrond.simplify250m <- st_simplify(Arrondissements, 
                                   preserveTopology = TRUE, 
                                   dTolerance = 250)
Arrond.simplify500m <- st_simplify(Arrondissements, 
                                   preserveTopology = TRUE, 
                                   dTolerance = 500)
Arrond.simplify1000m <- st_simplify(Arrondissements, 
                                    preserveTopology = TRUE, 
                                    dTolerance = 1000)
Arrond.simplify2000m <- st_simplify(Arrondissements, 
                                    preserveTopology = TRUE, 
                                    dTolerance = 2000)

Figure 1.9: Simplification des contours de géométries

Pour remédier au problème des frontières non conservées, utilisez l’algorithme de Visvalingam et Whyatt (1993) avec la fonction ms_simplify du package rmapshaper (figure 1.10), tel qu’illustré dans le code ci-dessous. À titre de rappel, pour l’installer et le charger sur votre ordinateur, tapez dans la console : install.packages("rmapshaper") et library("rmapshaper"). Le paramètre keep permet de définir la proportion de points à retenir : plus sa valeur est faible, plus la simplification est importante.

Figure 1.10: Simplification des contours avec l’algorithme de Visvalingam–Whyatt

1.2.2.6 Enveloppe convexe (convex hull)

Le code ci-dessous permet de créer l’enveloppe convexe pour des points (figure 1.11). Notez que cette fonction peut également s’appliquer à des lignes et à des polygones. Elle correspond aux outils Enveloppe convexe de QGIS et Feature to Point (avec l'option Convex hull) d’ArcGIS Pro.

## Enveloppe convexe autour des points GPS
PointsGPS.Convexhull <- st_convex_hull(st_union(PointsGPS))

Figure 1.11: Enveloppe convexe autour de points

1.2.2.7 Enveloppe concave (concave hull)

Une extension possible du polygone convexe est le polygone concave qui a une superficie plus réduite. Il n’existe pas de fonction dans sf qui l’implémente. Il faut donc installer un package supplémentaire, soit concaveman.

library(concaveman)
## Convex hull autour des points GPS
PointsGPS.Concavhull <- concaveman(PointsGPS)

Figure 1.12: Enveloppe concave autour de points

Notez que comparativement au polygone convexe (figure 1.12), le polygone concave peut auvoir plus d’une solution possible (lire l’article suivant). Plus spécifiquement, il faut choisir son degré de concavité. Dans la fonction concaveman::concaveman, le paramètre concavity prend une valeur numérique, qui, si elle tend vers l’infini, produit un polygone convexe (figure 1.13).

library(ggpubr)
# test avec plusieurs valeur de concavité
concav_values <- c(1,1.5,3,8)
plots <- lapply(concav_values, function(i){
  Concavhull <- concaveman(PointsGPS, concavity = i)
  this_plot <- ggplot()+
    geom_sf(data = Concavhull)+
    geom_sf(data = PointsGPS)+
    labs(subtitle = paste0("Concavité : ",i))+
      theme(axis.text.x = element_blank(),
            axis.text.y = element_blank(),
            axis.ticks = element_blank())
  return(this_plot)
})
ggarrange(plotlist = plots)

Figure 1.13: Enveloppe concave autour de points

Dans QGIS, il existe plusieurs plugins permettant de générer des enveloppes concaves, ainsi qu’une fonction installée de base avec GRASS (v.concave.hull).

1.2.3 Fonctions d’opérations géométriques entre deux couches

Les opérations entre deux couches sont bien connues et largement utilisées dans les SIG. Bien entendu, plusieurs fonctions de ce type sont disponibles dans sf et renvoient une nouvelle couche géographique sf :

• st_intersection(x, y) génère l’intersection entre les géométries de deux couches. À ne pas confondre avec la fonction st_intersects(x, y) qui permet de construire une requête spatiale.

• st_union(x, y) génère l’union entre les géométries de deux couches.

• st_difference(x, y) crée une géométrie à partir de x qui n’est pas en intersection avec y.

• st_sym_difference(x, y) crée une géométrie représentant les portions des géométries x et y qui ne s’intersectent pas.

• st_crop(x, y, xmin, ymin, xmax, ymax) extrait les géométries de x comprises dans un rectangle.

En guise de comparaison, toutes ces fonctions sont disponibles dans la boîte à outils de traitement de QGIS (dans le groupe recouvrement de vecteur) et les outils de la catégorie Overlay du Geoprocessing d’ArcGIS Pro. Le code ci-dessous illustre comment réaliser des intersections et des unions entre deux couches polygonales.

## Importation des deux couches
polysX <- st_read("data/chap01/shp/PolyX.shp", quiet = TRUE)
polysY <- st_read("data/chap01/shp/PolyY.shp", quiet = TRUE)
## Intersection des deux couches
## Les géométries récupèrent les attributs des deux couches
Inter.XY <- st_intersection(polysX, polysY)
head(Inter.XY)

Simple feature collection with 2 features and 2 fields
Geometry type: POLYGON
Dimension:     XY
Bounding box:  xmin: -8006904 ymin: 5684822 xmax: -8006602 ymax: 5685184
Projected CRS: WGS 84 / Pseudo-Mercator
  X_id Y_id                       geometry
1  X.a  Y.d POLYGON ((-8006753 5684838,...
2  Y.b  Y.d POLYGON ((-8006788 5684908,...

## Intersection entre deux couches préalablement fusionnées : 
## Le résutat est une seule géométrie
Inter.XYUnion <- st_intersection(st_union(polysX), st_union(polysY))
## Union des deux couches
Union.XY <- st_union(st_union(polysX), st_union(polysY))

La fonction st_intersection peut aussi être utilisée comme la méthode clip dans un SIG (ArcGIS Pro ou QGIS). En guise d’exemple, dans le code ci-dessous, nous extrayons les points GPS localisés sur le territoire de la ville de Sherbrooke (figure 1.14).

# Nous nous assurons que les deux couches ont la même projection
PointsGPS <- st_transform(PointsGPS, st_crs(Arrond.Union))
# Extraction des points
PointsGPS.Sherb <- st_intersection(PointsGPS, Arrond.Union)
# Visualisation avant et après
Carte1 <- ggplot()+geom_sf(data = Arrond.Union)+geom_sf(data = PointsGPS)+
          labs(subtitle = "Avant l'intersection")+
          theme(axis.text.x = element_blank(),
                axis.text.y = element_blank(),
                axis.ticks = element_blank())
Carte2 <- ggplot()+geom_sf(data = Arrond.Union)+geom_sf(data = PointsGPS.Sherb)+
          labs(subtitle = "Après l'intersection")+
          theme(axis.text.x = element_blank(),
                axis.text.y = element_blank(),
                axis.ticks = element_blank())
ggarrange(Carte1, Carte2, ncol = 2, nrow = 1)

Figure 1.14: Fonction st_intersection() équivalente à la méthode clip dans un SIG

Quelques lignes de code suffisent pour générer les différences de superposition entre les géométries de couches géographiques (figure 1.15).

## Différences entre deux couches
Diff.XY <- st_difference(st_union(polysX), st_union(polysY))
Diff.YX <- st_difference(st_union(polysY), st_union(polysX))
Diff.symXY <- st_sym_difference(st_union(polysY), st_union(polysX))

tmap_mode("plot")
MapInterU <- tm_shape(Zone)+tm_fill(col = NA, alpha = 0, border.col = NA, lwd = 0)+
tm_shape(Inter.XYUnion)+tm_polygons(col = "tomato4", alpha = .5, 
                            border.col ="black", lwd = 1)

MapDiffXY <- tm_shape(Zone)+tm_fill(col = NA, alpha = 0, border.col = NA, lwd = 0)+
             tm_shape(Diff.XY)+
             tm_polygons(col = "red", alpha = .5,border.col ="black", lwd = 1)+
             tm_layout(main.title = "st_difference(st_union(polysX), st_union(polysY))", 
                       main.title.size = .8)

MapDiffYX <- tm_shape(Zone)+tm_fill(col = NA, alpha = 0, border.col = NA, lwd = 0)+
             tm_shape(Diff.YX)+
             tm_polygons(col = "yellow", alpha = .5,border.col ="black", lwd = 1)+
             tm_layout(main.title = "st_difference(st_union(polysY), st_union(polysX))", 
                       main.title.size = .8)

MapSymDiffYX <- tm_shape(Zone)+tm_fill(col = NA, alpha = 0, border.col = NA, lwd = 0)+
             tm_shape(Diff.symXY)+
             tm_polygons(col = "green", alpha = .5,border.col ="black", lwd = 1)+
             tm_layout(main.title = "st_sym_difference(st_union(polysY), st_union(polysX))",
                       main.title.size = .8)

tmap_arrange(MapZone, MapDiffXY, MapDiffYX, MapSymDiffYX, ncol=2, nrow=2)

Figure 1.15: Différences de superposition entre des géométries de différentes couches

1.2.4 Fonctions de mesures géométriques et de récupération des coordonnées géographiques

Les principales fonctions de mesures géométriques et de coordonnées géographiques sont :

• st_area(x) calcule la superficie des polygones ou des multipolygones d’une couche sf .

• st_length(x) calcule la longueur des lignes ou des polylignes d’une couche sf .

• st_distance(x, y) calcule la distance 2D entre deux objets sf, exprimée dans le système de coordonnées de référence.

• st_coordinates(x) renvoie les coordonnées géographiques de géométries.

Ci-dessous, nous affichons les superficies des quatre arrondissements, puis nous enregistrons les superficies en m² et en km² dans deux nouveaux champs dénommés SupM2 et SupKm2.

## Superficie des polygones des arrondissements
st_area(Arrondissements)

Units: [m^2]
[1] 477791738 119343215  58289370  87034244

## Ajout de champs de superficie dans la table attributaire
Arrondissements$SupM2 <- as.numeric(st_area(st_transform(Arrondissements, crs = 2949)))
Arrondissements$SupKm2 <- as.numeric(st_area(st_transform(Arrondissements, crs = 2949)))/1000000
head(Arrondissements, n=2)

Simple feature collection with 2 features and 4 fields
Geometry type: POLYGON
Dimension:     XY
Bounding box:  xmin: -8027109 ymin: 5668860 xmax: -8000502 ymax: 5704391
Projected CRS: WGS 84 / Pseudo-Mercator
  NUMERO                                                         NOM
1      1 Arrondissement de Brompton–Rock Forest–Saint-Élie–Deauville
2      4                                  Arrondissement des Nations
                        geometry     SupM2    SupKm2
1 POLYGON ((-8005013 5702777,... 235580454 235.58045
2 POLYGON ((-8005680 5690860,...  58861606  58.86161

De manière très semblable, calculons la longueur de géométries étant des lignes ou des multilignes.

## Longueurs en mètres
PistesCyclables$longMetre <- as.numeric(st_length(st_transform(PistesCyclables, crs = 2949)))
PistesCyclables$longKm <- as.numeric(st_length(st_transform(PistesCyclables, crs = 2949)))/10000
head(PistesCyclables, n=2)

Simple feature collection with 2 features and 5 fields
Geometry type: MULTILINESTRING
Dimension:     XY
Bounding box:  xmin: -8010969 ymin: 5666202 xmax: -7997972 ymax: 5697954
Projected CRS: WGS 84 / Pseudo-Mercator
                       NOM OBJECTID SHAPE__Len                       geometry
1     Axe de la Massawippi        1   13944.09 MULTILINESTRING ((-8010969 ...
2 Axe de la Saint-François        2   19394.28 MULTILINESTRING ((-8001909 ...
  longMetre    longKm
1  9807.769 0.9807769
2 13602.324 1.3602324

Pour calculer la longueur d’un périmètre, il faut préalablement récupérer son contour avec la méthode st_boundary, puis calculer la longueur avec st_length.

## Conversion des polygones en lignes
Arrond.Contour <- st_boundary(Arrondissements)
## Calcul de la longueur et enregistrement dans deux nouveaux champs
Arrondissements$PerimetreMetre <- as.numeric(st_length(Arrond.Contour))
Arrondissements$PerimetreKm <- as.numeric(st_length(Arrond.Contour)) / 1000
head(Arrondissements)

Simple feature collection with 4 features and 6 fields
Geometry type: POLYGON
Dimension:     XY
Bounding box:  xmin: -8027109 ymin: 5668860 xmax: -7993013 ymax: 5704391
Projected CRS: WGS 84 / Pseudo-Mercator
  NUMERO                                                         NOM
1      1 Arrondissement de Brompton–Rock Forest–Saint-Élie–Deauville
2      4                                  Arrondissement des Nations
3      3                               Arrondissement de Lennoxville
4      2                                Arrondissement de Fleurimont
                        geometry     SupM2    SupKm2 PerimetreMetre PerimetreKm
1 POLYGON ((-8005013 5702777,... 235580454 235.58045      143771.63   143.77163
2 POLYGON ((-8005680 5690860,...  58861606  58.86161       50476.65    50.47665
3 POLYGON ((-7993443 5684778,...  28776861  28.77686       43531.03    43.53103
4 POLYGON ((-7999483 5693167,...  42882506  42.88251       44172.25    44.17225

Calculons désormais la distance 2D (euclidienne) entre les centres des arrondissements. Nous utilisons donc la fonction st_distance(x), puisque nous avons une seule couche (x = Arrond.pointpoly).

## Longueurs en mètres
st_distance(Arrond.pointpoly)

Units: [m]
         1         2         3         4
1     0.00 10458.989 21787.479 18047.846
2 10458.99     0.000 11555.203  8627.962
3 21787.48 11555.203     0.000  9622.735
4 18047.85  8627.962  9622.735     0.000

Admettons que nous souhaitons calculer la distance entre les centres des quatre arrondissements et l’hôtel de ville de Sherbrooke dont les coordonnées en degrés (WGS84, EPSG : 4326) sont les suivantes : -71.89306, 45.40417. Nous utilisons alors la fonction st_distance(x, y) dans laquelle les paramètres x et y sont les arrondissements et l’hôtel de ville. Quelques lignes de code suffisent à créer une couche pour l’hôtel de ville, à calculer les distances et à les stocker dans un nouveau champ attributaire de la couche arrondissement.

## Création d'un objet sf pour l'hôtel de ville
HotelVille <- data.frame(ID = 1,
                         Nom = "Hôtel de ville",
                         lon = -71.89306,
                         lat = 45.40417)
HotelVille <- st_as_sf(HotelVille, coords = c("lon","lat"), crs = 4326)
head(HotelVille)

Simple feature collection with 1 feature and 2 fields
Geometry type: POINT
Dimension:     XY
Bounding box:  xmin: -71.89306 ymin: 45.40417 xmax: -71.89306 ymax: 45.40417
Geodetic CRS:  WGS 84
  ID            Nom                   geometry
1  1 Hôtel de ville POINT (-71.89306 45.40417)

## Nous nous assurons que les deux couches ont la même projection
HotelVille <- st_transform(HotelVille, st_crs(Arrond.pointpoly))
## Calcul des distances
Arrondissements$DistHVMetre <- as.numeric(st_distance(Arrond.pointpoly,HotelVille))
Arrondissements$DistHVKm <- as.numeric(st_distance(Arrond.pointpoly,
                                                   HotelVille)) / 1000
head(Arrondissements)

Simple feature collection with 4 features and 8 fields
Geometry type: POLYGON
Dimension:     XY
Bounding box:  xmin: -8027109 ymin: 5668860 xmax: -7993013 ymax: 5704391
Projected CRS: WGS 84 / Pseudo-Mercator
  NUMERO                                                         NOM
1      1 Arrondissement de Brompton–Rock Forest–Saint-Élie–Deauville
2      4                                  Arrondissement des Nations
3      3                               Arrondissement de Lennoxville
4      2                                Arrondissement de Fleurimont
                        geometry     SupM2    SupKm2 PerimetreMetre PerimetreKm
1 POLYGON ((-8005013 5702777,... 235580454 235.58045      143771.63   143.77163
2 POLYGON ((-8005680 5690860,...  58861606  58.86161       50476.65    50.47665
3 POLYGON ((-7993443 5684778,...  28776861  28.77686       43531.03    43.53103
4 POLYGON ((-7999483 5693167,...  42882506  42.88251       44172.25    44.17225
  DistHVMetre  DistHVKm
1   14661.518 14.661518
2    4662.164  4.662164
3    9058.677  9.058677
4    4050.374  4.050374

Il est fréquent de vouloir enregistrer les coordonnées géographiques dans des champs attributaires. Dans le code ci-dessous, nous créons deux champs (x et y) dans lesquels nous enregistrons les coordonnées géographiques des points au centre de la surface de chaque arrondissement. Pour ce faire, nous utilisons la méthode st_coordinates .

## Coordonnées des centres de la surface des polygones
xy <- st_coordinates(st_point_on_surface(Arrondissements))
head(xy)

            X       Y
[1,] -8017707 5686628
[2,] -8007570 5684053
[3,] -7997637 5678149
[4,] -7999683 5687552

## Enregistrement dans la couche Arrondissements. Notez que :
## xy[,1] signale de récupérer toutes les valeurs de la première colonne, soit X
## xy[,2] signale de récupérer toutes les valeurs de la deuxième colonne, soit Y
Arrondissements$X <- xy[,1] 
Arrondissements$Y <- xy[,2]

1.2.5 Jointures spatiales

En géomatique, il est fréquent de réaliser des jointures spatiales, soit une opération qui consiste à joindre les attributs d’une couche géographique à une autre à partir d’une relation spatiale. Prenons deux exemples construits avec les installations sportives et récréatives (couche InstallationSport) et les arrondissements de la ville de Sherbrooke (Arrondissements).

Premièrement, pour les installations sportives et récréatives (couche InstallationSport), nous souhaitons ajouter dans la table attributaire les champs NUMERO et NOM issus de la couche des arrondissements de la ville de Sherbrooke (Arrondissements). Grâce à ces deux champs, nous pouvons connaître dans quel arrondissement chaque installation sportive est située.

## Jointure spatiale avec le paramètre st_intersects
InstallS.join <- st_join(InstallationSport, Arrondissements, join = st_intersects)
## Visualisation des deux premiers enregistrements
head(InstallS.join, n=2)

Simple feature collection with 2 features and 16 fields
Geometry type: POINT
Dimension:     XY
Bounding box:  xmin: -8009681 ymin: 5686891 xmax: -8001939 ymax: 5696536
Projected CRS: WGS 84 / Pseudo-Mercator
   TYPE DETAIL                   NOM.x SURFACE ECLAIRAGE OBJECTID NUMERO
1 Aréna   <NA>    Aréna Eugène-Lalonde    <NA>      <NA>        1      2
2 Aréna   <NA> Aréna Philippe-Bergeron    <NA>      <NA>        2      1
                                                        NOM.y     SupM2
1                                Arrondissement de Fleurimont  42882506
2 Arrondissement de Brompton–Rock Forest–Saint-Élie–Deauville 235580454
     SupKm2 PerimetreMetre PerimetreKm DistHVMetre  DistHVKm        X       Y
1  42.88251       44172.25    44.17225    4050.374  4.050374 -7999683 5687552
2 235.58045      143771.63   143.77163   14661.518 14.661518 -8017707 5686628
                  geometry
1 POINT (-8001939 5686891)
2 POINT (-8009681 5696536)

## Suppression des champs utiles
InstallS.join[c("SupM2", "SupKm2", "PerimetreMetre", 
                       "PerimetreKm", "DistHVMetre",  "DistHVKm")] <- list(NULL)
## Modification des noms de champs : NOM.x et NOM.y
names(InstallS.join)[names(InstallS.join) == "NOM.x"] <- "NomInstallation"
names(InstallS.join)[names(InstallS.join) == "NOM.y"] <- "NomArrondissement"
head(InstallS.join, n=2)

Simple feature collection with 2 features and 10 fields
Geometry type: POINT
Dimension:     XY
Bounding box:  xmin: -8009681 ymin: 5686891 xmax: -8001939 ymax: 5696536
Projected CRS: WGS 84 / Pseudo-Mercator
   TYPE DETAIL         NomInstallation SURFACE ECLAIRAGE OBJECTID NUMERO
1 Aréna   <NA>    Aréna Eugène-Lalonde    <NA>      <NA>        1      2
2 Aréna   <NA> Aréna Philippe-Bergeron    <NA>      <NA>        2      1
                                            NomArrondissement        X       Y
1                                Arrondissement de Fleurimont -7999683 5687552
2 Arrondissement de Brompton–Rock Forest–Saint-Élie–Deauville -8017707 5686628
                  geometry
1 POINT (-8001939 5686891)
2 POINT (-8009681 5696536)

Deuxièmement, une autre jointure classique consiste à dénombrer les points compris dans des polygones, soit une opération SIG communément appelée POINT-IN-POLYGON.

## Sélection des points dans les polygones des arrondissements
## Notez que la relation spatiale pour la jointure est st_contains
## Nous aurions pu aussi utiliser st_intersects
Arrondissements$NbInstall = lengths(st_contains(Arrondissements, InstallationSport))
head(Arrondissements$NbInstall)

[1] 125 166  29 116

Autres relations spatiales à appliquer lors de la jointure spatiale

Avec le paramètre join de la méthode st_join, il est possible de spécifier la jointure spatiale avec différentes méthodes : st_contains_properly, st_contains, st_covered_by, st_covers, st_crosses, st_disjoint, st_equals_exact, st_equals, st_is_within_distance, st_nearest_feature,st_overlaps, st_touches et st_within.

N’hésitez pas à consulter la documentation de la fonction en tapant?st_join dans la console R.

1.2.6 Requêtes spatiales

Dans un logiciel SIG, la sélection d’entités spatiales par localisation est une opération courante, équivalente à Select By Location dans ArcGis Pro ou Sélection par localisation dans QGIS.

Le package sf permet de réaliser des requêtes spatiales avec notamment les méthodes suivantes :

• st_contains(x, y) renvoie les géométries de x qui contiennent celles de y. Cette fonction est donc l’inverse de st_within.

• st_disjoint(x, y) renvoie les géométries de x qui ne partagent aucune portion de celles de y. Cette fonction est donc l’inverse de st_intersects(x, y).

• st_equals(x, y) renvoie les géométries de x qui sont identiques à celles de y.

• st_intersects(x, y) renvoie les géométries de x qui partagent au moins une partie de celles de y. Elle est donc l’inverse de st_disjoints(x, y).

• st_nearest_feature(x, y) renvoie, pour chaque géométrie x, la géométrie de y qui est la plus proche.

• st_overlaps(x, y) cette fonction est très semblable à st_intersects(x, y). Toutefois, les types de géométries de x et de y doivent être identiques, c’est-à-dire deux couches de lignes ou de couches de polygones. Aussi, une géométrie ne peut pas contenir complètement l’autre comme avec st_within(x, y) et st_contains(x, y).

• st_touches(x, y) renvoie les géométries de x qui sont tangentes à celles de x sans qu’elles se chevauchent. Par exemple, deux arrondissements peuvent se toucher, c’est-à-dire qu’ils partagent une frontière commune sans que l’un chevauche l’autre.

• st_within(x, y) renvoie les géométries de x qui sont comprises intégralement dans celles de y. Cette fonction est donc l’inverse de st_contains(x, y).

• st_within_distance(x, y, dist =) renvoie les géométries de x qui sont situées à une certaine distance euclidienne de celles de y.

Modification de l’affichage du résultat de la requête spatiale : le paramètre sparse

Par défaut, le résultat d’une requête spatiale renvoie une liste d’indices pour les géométries x et y. Il est aussi possible de renvoyer la matrice complète entre x et y, avec les valeurs TRUE quand la relation spatiale est vérifiée et FALSE pour une situation inverse.

Prenons deux exemples pour illustrer le tout.

La figure ci-dessous représente les quatre arrondissements de la ville de Sherbrooke. Notez que les numéros correspondent aux indices des géométries.

  NUMERO                                                         NOM
1      1 Arrondissement de Brompton–Rock Forest–Saint-Élie–Deauville
2      4                                  Arrondissement des Nations
3      3                               Arrondissement de Lennoxville
4      2                                Arrondissement de Fleurimont

Appliquons une requête spatiale entre les arrondissements avec st_intersects et sparse = TRUE. Pour chaque arrondissement, nous obtenons une liste des arrondissements qui l’intersectent.

st_intersects(Arrondissements, Arrondissements, sparse = TRUE)

Sparse geometry binary predicate list of length 4, where the predicate
was `intersects'
 1: 1, 2, 4
 2: 1, 2, 3, 4
 3: 2, 3, 4
 4: 1, 2, 3, 4

Avec sparse = FALSE, nous obtenons une matrice complète de dimension 4 X 4 arrondissements. Nous constatons que l’arrondissement 1 intersecte lui-même (évidemment!) et les arrondissements 2 et 4, mais il n’intersecte pas le 3.

st_intersects(Arrondissements, Arrondissements, sparse = FALSE)

      [,1] [,2]  [,3] [,4]
[1,]  TRUE TRUE FALSE TRUE
[2,]  TRUE TRUE  TRUE TRUE
[3,] FALSE TRUE  TRUE TRUE
[4,]  TRUE TRUE  TRUE TRUE

Construisons des requêtes plus complexes comprenant deux couches.

Premièrement, écrivons une requête spatiale pour sélectionner les segments des pistes cyclables qui intersectent le parc du Mont-Bellevue. Pour ce faire, nous utilisons la fonction st_intersects avec l’argument sparse = FALSE et enregistrons le résultat dans un nouveau champ dénommé ParcMB.intersect qui prendra les valeurs TRUE ou FALSE.

## Intersection
RequeteSpatiale <- st_intersects(PistesCyclables, MontBellevue, sparse = FALSE)
head(RequeteSpatiale)

      [,1]
[1,] FALSE
[2,] FALSE
[3,] FALSE
[4,] FALSE
[5,] FALSE
[6,] FALSE

## Création d'un nouveau champ
PistesCyclables$ParcMB.intersect <- RequeteSpatiale[, 1]
head(PistesCyclables)

Simple feature collection with 6 features and 6 fields
Geometry type: MULTILINESTRING
Dimension:     XY
Bounding box:  xmin: -8010969 ymin: 5666202 xmax: -7997216 ymax: 5697954
Projected CRS: WGS 84 / Pseudo-Mercator
                       NOM OBJECTID  SHAPE__Len                       geometry
1     Axe de la Massawippi        1 13944.08678 MULTILINESTRING ((-8010969 ...
2 Axe de la Saint-François        2 19394.27693 MULTILINESTRING ((-8001909 ...
3   Axe du Ruisseau-Dorman        3 16337.23985 MULTILINESTRING ((-7999121 ...
4        Réseau utilitaire        4   467.23254 MULTILINESTRING ((-8000179 ...
5        Réseau utilitaire        5    15.57987 MULTILINESTRING ((-8004036 ...
6        Réseau utilitaire        6   823.83428 MULTILINESTRING ((-8003649 ...
    longMetre      longKm ParcMB.intersect
1  9807.76890 0.980776890            FALSE
2 13602.32404 1.360232404            FALSE
3 11469.13476 1.146913476            FALSE
4   327.46928 0.032746928            FALSE
5    10.95083 0.001095083            FALSE
6   578.59143 0.057859143            FALSE

## Nous constatons qu'un seul segment intersecte le parc
table(PistesCyclables$ParcMB.intersect)

FALSE  TRUE 
  272     1 

## Création d'une nouvelle couche pour la sélection
PistesCyclables.Selection <- PistesCyclables[PistesCyclables$ParcMB.intersect== TRUE, ]
## Visualisation
tmap_mode("view")
tm_shape(MontBellevue) + tm_fill(col="lightgreen")+ tm_borders(col = "black", lwd=2)+
tm_shape(PistesCyclables.Selection)+tm_lines(col="red", lwd=1)

Créons une deuxième requête spatiale pour sélectionner les points GPS situés à moins de cinq kilomètres de l’hôtel de ville de Sherbrooke avec la méthode st_is_within_distance.

## Requête spatiale
RequeteSpatiale <- st_is_within_distance(PointsGPS, HotelVille, 
                                         5000, sparse = FALSE)
## Ajout d'un champ pour la requête
PointsGPS$HotelVille2km <- RequeteSpatiale[, 1]
## Nous constatons que 17 points GPS sont à moins de 5 km
table(PointsGPS$HotelVille2km)

FALSE  TRUE 
   72    17 

## Création d'une nouvelle couche pour la sélection
PointsGPS.selection <- PointsGPS[PointsGPS$HotelVille2km== TRUE, ]
## Visualisation
tm_shape(PointsGPS.selection) + tm_dots(col="red", size = .05)+
tm_shape(HotelVille)+tm_dots(col="black", size = .25)

Finalement, avec la méthode st_within, nous constatons que seuls deux points GPS sont situés dans le parc du Mont-Bellevue.

## Requête spatiale
RequeteSpatiale <- st_within(st_transform(PointsGPS, st_crs(MontBellevue)),
                             MontBellevue, sparse = FALSE)
table(RequeteSpatiale[,1])

FALSE  TRUE 
   87     2 

1.2.7 Manipulation des données attributaires

Dans cette section, nous verrons comment importer une table attributaire, puis la joindre à une couche géographique, ajouter et calculer de nouveaux champs et réaliser des requêtes attributaires.

1.2.7.1 Importation d’une table attributaire

Joindre les attributs d’une table externe à une couche vectorielle sf

Dans un SIG, joindre une table à une couche géographique vectorielle est une opération courante. Par exemple, il est fréquent de joindre des données socioéconomiques issues d’un recensement à une couche géographique (divisions de recensement, subdivisions de recensement, secteurs de recensement, aires de diffusion, etc.).

Pour ce faire, vous devez importer les données dans un DataFrame de R. Ces données peuvent être stockées dans différents formats de fichiers (texte délimité par des virgules (extension csv), dBase (dbf), Excel (xlsx)) ou dans des fichiers provenant de logiciels statistiques commerciaux comme Stata, SAS et SPSS (dta, sas7bdat, sav).

Dans cette section, nous voyons seulement l’importation de fichiers texte délimités par des virgules, de fichiers Excel et dBase. Concernant ce dernier type de fichier, notez que la table attributaire d’une couche Esri Shapefile est stockée dans un fichier dBase! Il peut être intéressant d’importer la table sans les géométries.

Pour une description détaillée de l’importation d’autres fichiers (entre autres Stata, SAS et SPSS), consultez la section intitulée Manipulation d’un DataFrame (Apparicio et Gelb 2022).

Dans le code ci-dessous, nous voyons comment importer trois types de fichiers :

• read.csv(file) pour importer un fichier délimité par des virgules. Cette fonction est de base avec R, ce qui signifie qu’elle ne nécessite pas l’installation d’un package.

• read.dbf(file) pour importer un fichier dBase. Cette fonction est rattachée au package foreign que vous devez installer si ce n’est pas déjà fait (commande install.packages("foreign")) et le charger (commande library("foreign")).

• read.xlsx(file) pour importer un fichier Excel. Cette fonction est rattachée au package xlsx que vous devez installer si ce n’est pas déjà fait (commande install.packages("xlsx")) et le charger (commande library("xlsx")).

library("xlsx")      # package pour importer des fichiers Excel
library("foreign")   # package pour importer des fichiers dBase
## Importation du fichier csv
t1 <- Sys.time()
dfCSV <- read.csv(file = "data/chap01/tables/SRQC2021.csv",
                    header = TRUE,
                    dec = ".",    # séparateur de décimales qui peut être remplacé par ,
                    sep = ","     # séparateur des champs qui peut être remplacé par ;
                    )
t2 <- Sys.time()
cat("temps de traitement (CSV) : ", 
    as.numeric(difftime(t2,t1,units="secs")),
    " secondes")

temps de traitement (CSV) :  0.03482509  secondes

## Importation d'un fichier Excel avec le nom de fichier et de la feuille Excel
## sheetIndex = 1 signale l'importation de la première feuille Excel
t1 <- Sys.time()
dfExcel <- read.xlsx(file = "data/chap01/tables/ADSRQC2021.xlsx",
                      sheetIndex = 2)
t2 <- Sys.time()
cat("temps de traitement (Excel) : ", 
    as.numeric(difftime(t2,t1,units="secs")),
    " secondes")

temps de traitement (Excel) :  11.75225  secondes

## Importation du fichier dBase
t1 <- Sys.time()
dfDbf <- read.dbf(file = "data/chap01/tables/ADQC2021.dbf")
t2 <- Sys.time()
cat("temps de traitement (dBase) : ", 
    as.numeric(difftime(t2,t1,units="secs")),
    " secondes")

temps de traitement (dBase) :  0.174763  secondes

Exportation du fichier Excel dans un fichier texte

Le temps nécessaire pour importer un fichier Excel est bien plus long que pour des fichiers texte et dBase! Par conséquent, si vous travaillez avec Excel, il est vivement conseillé de l’exporter vers un fichier texte (dans Excel, Fichier/Enregistrer sous/type de fichier CSV).

Quelques lignes suffisent pour explorer la structure des données importées avec les fonctions nrow, ncol, colnames (respectivement le nombre de lignes, le nombre de colonnes et les noms des colonnes du dataframe).

## Nombre de lignes et de colonnes
nrow(dfCSV)

[1] 2245

ncol(dfCSV)

[1] 40

cat("le DataFrame dfCSV a", nrow(dfCSV), "lignes (observations)",
    'et', ncol(dfCSV), "colonnes\n")

le DataFrame dfCSV a 2245 lignes (observations) et 40 colonnes

## Noms des champs
colnames(dfCSV)

 [1] "SRIDU"                     "PopTotAge"                
 [3] "Pop0_14"                   "Pop15_64"                 
 [5] "Pop65plus"                 "TotalLog"                 
 [7] "MaisonIndiv"               "MaisonJumulee"            
 [9] "MaisonRangee"              "AppartDuplex"             
[11] "AppartMoins5E"             "Appart5EtPlus"            
[13] "AutreMaisonIndivAttenante" "LogementMobile"           
[15] "TotalMenag"                "Menage1pers"              
[17] "Menage2pers"               "Menage3pers"              
[19] "Menage4pers"               "Menage5pPlus"             
[21] "RevMedMenage"              "PopTotMFRApI"             
[23] "PopTotMFR"                 "PopTotMFRPct"             
[25] "TotalMenag2"               "Proprietaire"             
[27] "Locataire"                 "TotalLog2"                
[29] "Log1960ouAv"               "Log1961_80"               
[31] "Log1981_90"                "Log1991_00"               
[33] "Log2001_05"                "Log2006_10"               
[35] "Log2011_15"                "Log2016_21"               
[37] "ValeurMedLog"              "ValeurMoyLog"             
[39] "LoyerMedian"               "LoyerMoyen"               

## Affichage des deux premières observations
head(dfCSV, n=2)

                                                      SRIDU PopTotAge Pop0_14
1 4470001.01 (SR), Drummondville (RMR) (4470001.01) (00000)      5080     810
2 4470001.02 (SR), Drummondville (RMR) (4470001.02) (00000)      3400     175
  Pop15_64 Pop65plus TotalLog MaisonIndiv MaisonJumulee MaisonRangee
1     3285       985     2280        1290           185          210
2     1305      1920     1815         155            75           85
  AppartDuplex AppartMoins5E Appart5EtPlus AutreMaisonIndivAttenante
1           70           415             0                        15
2           15          1485             0                         5
  LogementMobile TotalMenag Menage1pers Menage2pers Menage3pers Menage4pers
1            100       2285         705         895         325         225
2              0       1810         985         670         100          45
  Menage5pPlus RevMedMenage PopTotMFRApI PopTotMFR PopTotMFRPct TotalMenag2
1          130        69000         5085       520         10.2        2295
2           15        47600         2885       545         18.9        1820
  Proprietaire Locataire TotalLog2 Log1960ouAv Log1961_80 Log1981_90 Log1991_00
1         1445       850      2295         115        590        535        485
2          485      1335      1820          50        310        375        405
  Log2001_05 Log2006_10 Log2011_15 Log2016_21 ValeurMedLog ValeurMoyLog
1        155         70         75        265       250000       250200
2        215        200        120        140       250000       305000
  LoyerMedian LoyerMoyen
1         695        742
2         740        737

1.2.7.2 Jointure attributaire avec la couche géographique sf

Les données importées dans la table attributive proviennent du recensement de Statistique Canada de 2021 et sont ancrées au niveau des secteurs de recensement (SR) des régions métropolitaines de recensement (RMR) et des agglomérations de recensement (AR) du Québec. Pour les SR de la RMR de Sherbrooke, les données de la couche géométrique sont importées à partir d’un fichier shapefile. Aussi, nous constatons que les deux sources de données ont un champ commun SRIDU, soit l’identifiant unique des SR, mais que l’information y est présentée différemment :

• Dans la couche géographique SR.RMRSherb (objet sf), nous avons une observation avec la valeur 4470001.01, soit un champ avec dix caractères.

• Dans la table attributaire dfCSV (DataFrame), nous avons une observation avec la valeur 4470001.01 (SR), Drummondville (RMR) (4470001.01) (00000).

Par conséquent, avant d’appliquer une jointure, nous modifions le champ SRIDU de ce DataFrame afin qu’il ait aussi dix caractères avec la ligne de code suivante : dfCSV$SRIDU <- substr(dfCSV$SRIDU, 1, 10). De la sorte, nous récupérons uniquement les dix premiers caractères.

Finalement, la jointure est réalisée avec la fonction merge avec laquelle nous spécifions le résultat de la jointure (SR.RMRSherbDonnees), la couche géographique (SR.RMRSherb), la table attributaire (dfCSV) et le champ commun aux deux avec l’option (by ="SRIDU") :

SR.RMRSherbDonnees <- merge(SR.RMRSherb, dfCSV, by = "SRIDU").

## Importation des SR de la RMR de Sherbrooke
SR.RMRSherb <- st_read(dsn = "data/chap01/gpkg/Recen2021Sherbrooke.gpkg", 
                       layer = "SherbSR", quiet=TRUE)
## Visualisation des premiers enregistrements
head(as.data.frame(SR.RMRSherb), n=2)

                IDUGD      SRIDU   SRNOM SUPTERRE PRIDU SRpop_2021 SRtlog_2021
1 2021S05074330001.00 4330001.00 0001.00   3.1882    24       5637        2918
2 2021S05074330002.00 4330002.00 0002.00   0.8727    24       1868        1169
  SRrhlog_2021 RMRcode   HabKm2                           geom
1         2756     433 1768.082 MULTIPOLYGON (((7764998 127...
2         1063     433 2140.484 MULTIPOLYGON (((7763361 127...

head(dfCSV, n=2)

                                                      SRIDU PopTotAge Pop0_14
1 4470001.01 (SR), Drummondville (RMR) (4470001.01) (00000)      5080     810
2 4470001.02 (SR), Drummondville (RMR) (4470001.02) (00000)      3400     175
  Pop15_64 Pop65plus TotalLog MaisonIndiv MaisonJumulee MaisonRangee
1     3285       985     2280        1290           185          210
2     1305      1920     1815         155            75           85
  AppartDuplex AppartMoins5E Appart5EtPlus AutreMaisonIndivAttenante
1           70           415             0                        15
2           15          1485             0                         5
  LogementMobile TotalMenag Menage1pers Menage2pers Menage3pers Menage4pers
1            100       2285         705         895         325         225
2              0       1810         985         670         100          45
  Menage5pPlus RevMedMenage PopTotMFRApI PopTotMFR PopTotMFRPct TotalMenag2
1          130        69000         5085       520         10.2        2295
2           15        47600         2885       545         18.9        1820
  Proprietaire Locataire TotalLog2 Log1960ouAv Log1961_80 Log1981_90 Log1991_00
1         1445       850      2295         115        590        535        485
2          485      1335      1820          50        310        375        405
  Log2001_05 Log2006_10 Log2011_15 Log2016_21 ValeurMedLog ValeurMoyLog
1        155         70         75        265       250000       250200
2        215        200        120        140       250000       305000
  LoyerMedian LoyerMoyen
1         695        742
2         740        737

## Modification du champ SRIDU du DataFrame dfCSV
dfCSV$SRIDU <- substr(dfCSV$SRIDU, 1, 10)
## Jointure attributaire avec la fonction merge
SR.RMRSherbDonnees <- merge(SR.RMRSherb, 
                           dfCSV, 
                           by = "SRIDU")

Jointure avec deux champs ayant des noms différents

En résumé, une jointure attributaire s’écrit :

NouvelObjetSf <- merge(X, Y, by = "Nom du champ commun pour la jointure")

avec X et Y étant respectivement l’objet sf (couche géographique) et la table attributaire à joindre. Si les champs pour la jointure ont des noms différents, il est possible d’écrire :

NouvelObjetSf <- merge(X, Y, by.x = "Champ X pour la jointure", by.y = "Champ Y pour la jointure")

Ce type de jointure conserve uniquement les observations qui sont communes à la couche géographique et à la table attributaire. Concrètement, si une couche comprend 100 entités spatiales et la table attributaire uniquement 80 observations, la couche résultante (NouvelObjetSf) aura uniquement 80 entités spatiales (bien entendu, quand les valeurs concordent…).

Lorsque vous souhaitez quand même conserver toutes les entités spatiales de la couche géographique de départ, écrivez :

NouvelObjetSf <- merge(X, Y, by = "Nom du champ commun pour la jointure", all.x = TRUE)

Dans la nouvelle couche Sf, les entités spatiales de X qui n’ont pas été appariées avec les observations de la table attributaire Y auront des valeurs nulles (NA) pour les champs de X ajoutés au NouvelObjetSf.

Pour obtenir plus d’informations sur les différentes variantes d’une jointure, tapez ?merge dans la console.

1.2.7.3 Ajout et calcul de champs

Dans la section 1.2.4, nous avons vu comment ajouter des champs relatifs à la géométrie (aire, longueur, distance, coordonnées de centroïdes). Dans un SIG, il est courant de calculer de nouveaux champs à partir de champs existants dans la table attributaire (par exemple, avec les outils Calculatrice de champ dans QGIS ou Calculate Field dans ArcGIS Pro).

Ce type de traitement est aussi très simple à réaliser dans R. Pour ce faire, nous utilisons des opérateurs mathématiques, relationnels et logiques comme dans n’importe quel logiciel de SIG. En guise d’exemple, nous calculons ci-dessous les pourcentages d’enfants de moins de 15 ans et de locataires. Ces pourcentages sont arrondis à deux décimales avec la fonction round.

## Création et cacul de nouveau champs
SR.RMRSherbDonnees$PctPop0_14 <- round(SR.RMRSherbDonnees$Pop0_14 / 
                                     SR.RMRSherbDonnees$PopTotAge * 100, 2)

SR.RMRSherbDonnees$PctLocataire <- round(SR.RMRSherbDonnees$Locataire / 
                                     SR.RMRSherbDonnees$TotalMenag2 * 100, 2)

1.2.7.4 Requêtes attributaires

Dans un SIG, il est fréquent de réaliser une requête attributaire pour explorer les données (par exemple, avec les outils Select By Attributes dans ArcGIS Pro et Sélection avec expression dans QGIS) et exporter le résultat de la requête dans une nouvelle couche (Export Features dans ArcGIS Pro et Sauvegarder les entités sélectionnées sous…).

Dans le code ci-dessous, vous trouverez plusieurs exemples de requêtes attributaires. Remarquez que les résultats des requêtes sont enregistrés dans de nouveaux objets sf (couches géographiques) dénommés Requete1 à Requete5.

## Sélection de l'axe cyclable de la Magog
#############################################
# Affichage des valeurs uniques pour le champ NOM de la couche PistesCyclables
unique(PistesCyclables$NOM)

 [1] "Axe de la Massawippi"         "Axe de la Saint-François"    
 [3] "Axe du Ruisseau-Dorman"       "Réseau utilitaire"           
 [5] "Tronçon fermé temporairement" "Détour"                      
 [7] "Axe de la Magog"              "Axe du Ruisseau-Kee"         
 [9] "Axe de la Magog Sud"          NA                            
[11] "Axe du Sommet"               

## Requête attributaire et enregistrement du résultat dans un nouvel objet sf
Requete1 <- subset(PistesCyclables, NOM == "Axe de la Magog")
cat(nrow(Requete1), "enregistrements sélectionnés sur", nrow(PistesCyclables))

15 enregistrements sélectionnés sur 273

## Si vous souhaitez connaître uniquement le nombre d'enregistrements sélectionnés
## sans créer un nouvel objet sf, il suffit d'écrire :
nrow(subset(PistesCyclables, NOM == "Axe de la Magog"))

[1] 15

## Sélection des SR dont la moitié ou plus des logements sont en location
##########################################################################
## Sommaire statistique sur le champ pourcentage de locataires
summary(SR.RMRSherbDonnees$PctLocataire)

   Min. 1st Qu.  Median    Mean 3rd Qu.    Max. 
   6.92   18.03   41.63   43.81   65.95   93.83 

## Requête attributaire et enregistrement du résultat dans un nouvel objet sf
Requete2 <- subset(SR.RMRSherbDonnees, PctLocataire >= 50)
cat(nrow(Requete2), "enregistrements sélectionnés sur", nrow(SR.RMRSherbDonnees))

20 enregistrements sélectionnés sur 50

## Sélection des installations sportives avec un éclairage dans 
## l'arrondissement des Nations (deux critères dans la requête)
##########################################################################
unique(InstallS.join$NomArrondissement)

[1] "Arrondissement de Fleurimont"                               
[2] "Arrondissement de Brompton–Rock Forest–Saint-Élie–Deauville"
[3] "Arrondissement des Nations"                                 
[4] "Arrondissement de Lennoxville"                              

table(InstallS.join$ECLAIRAGE)

Non Oui 
 46  85 

## Requête attributaire avec un opérateur AND (&)
Requete3 <- subset(InstallS.join,
                   NomArrondissement == "Arrondissement des Nations" & 
                   ECLAIRAGE == "Oui")
cat(nrow(Requete3), "enregistrements sélectionnés sur", nrow(InstallS.join))

30 enregistrements sélectionnés sur 436

## Sélection des SR avec deux critères et un opérateur OR (|)
##########################################################################
## Sommaires statistiques sur deux champs
summary(SR.RMRSherbDonnees$LoyerMoyen)

   Min. 1st Qu.  Median    Mean 3rd Qu.    Max. 
  570.0   679.5   729.0   768.4   847.5  1200.0 

summary(SR.RMRSherbDonnees$ValeurMedLog)

   Min. 1st Qu.  Median    Mean 3rd Qu.    Max. 
 200000  235500  250000  272520  300000  476000 

## Requête attributaire avec un opérateur OR 
Requete4 <- subset(SR.RMRSherbDonnees,
                   LoyerMoyen < 700 | ValeurMedLog < 250000)
cat(nrow(Requete4), "enregistrements sélectionnés sur", nrow(SR.RMRSherbDonnees))

27 enregistrements sélectionnés sur 50

## Sélection de différents types d'installations sportives
##########################################################################
unique(InstallS.join$TYPE)

 [1] "Aréna"                          "Tir à l'arc"                   
 [3] "Pétanque"                       "Jeu de galets"                 
 [5] "Planche à roulettes"            "Préau et plancher de danse"    
 [7] "Patinoire à bandes mobiles"     "Surface, anneau ou étang glacé"
 [9] "Patinoire à bandes fixes"       "Plage"                         
[11] "Jeu d'eau"                      "Piste multifonctionnelle"      
[13] "Glissade sur tube"              "Jeu de fers"                   
[15] "Piscine"                        "Tennis"                        
[17] "Baseball"                       "Basketball"                    
[19] "Football"                       "Volleyball"                    
[21] "Ultimate frisbee"               "Pickleball"                    
[23] "Soccer"                         "Jeu modulaire"                 

## Requête attributaire avec un opérateur %in%
Requete5 <- subset(InstallS.join,
                             TYPE %in% c("Aréna", "Piscine", "Jeu d'eau"))
cat(nrow(Requete5), "enregistrements sélectionnés sur", nrow(InstallS.join))

26 enregistrements sélectionnés sur 436

1.3 Manipulation de données matricielles (raster)

En géomatique, les données matricielles (raster) sont une représentation de l’information spatiale sous forme d’une grille rectangulaire composée de cellules élémentaires de taille identique appelées pixels, soit une image. Chaque pixel a une valeur pour une caractéristique spécifique, comme l’altitude, la température, l’utilisation du sol, etc. Les données matricielles sont couramment employées dans les systèmes d’information géographique (SIG) pour la cartographie, l’analyse et la prise de décision en géomatique.

Dans cette section, nous abordons uniquement des fonctions simples de manipulation de données matricielles, notamment le mosaïquage et découpage d’images, et les requêtes attributaires sur des images.

1.3.1 Mosaïquage et découpage d’images

Une fois plusieurs images importées, il est fréquent de vouloir les fusionner. Pour ce faire, nous utilisons deux méthodes du package terra :

• terra::merge fusionne plusieurs images (objets de type SpatRasters) pour former un nouvel objet SpatRasters dont l’étendue est recalculée en fonction des images fusionnées. Par contre, quand les images se chevauchent, les valeurs des pixels dans les zones de chevauchement seront prises dans le même ordre que les images.

• terra::mosaic fusionne aussi plusieurs images. Toutefois, dans les zones de chevauchement, les moyennes des pixels sont calculées. Selon la documentation de terra, cette méthode serait plus rapide que la précédente. Dans le code ci-dessous, nous fusionnons les feuillets de modèles numériques d’altitude (MNA) importés dans la section 1.1.2.

## Les GeoTIFF importés avec terra sont bien des SpatRaster
class(f21e05_101)

[1] "SpatRaster"
attr(,"package")
[1] "terra"

## Création d'une liste pour les cinq feuillets SpatRaster
rlist <- list(f21e05_101, f21e05_201, f31h08_102,
              f31h08_202, f21e12_101)
rsrc <- sprc(rlist)
## Création de la mosaïque
MosaicSherb <- mosaic(rsrc)
MosaicSherb

class       : SpatRaster 
dimensions  : 4187, 5575, 1  (nrow, ncol, nlyr)
resolution  : 9e-05, 9e-05  (x, y)
extent      : -72.25087, -71.74913, 45.24907, 45.6259  (xmin, xmax, ymin, ymax)
coord. ref. : lon/lat NAD83 (EPSG:4269) 
source(s)   : memory
varname     : f21e05_101 
name        : f21e05_101 
min value   :   123.7184 
max value   :   845.0474 

Vous constatez ci-dessus que la projection des images est lon/lat NAD83 (EPSG:4269).

D’autres fonctions permettent de découper une image en fonction d’une autre image (objet SpatRaster de terra) ou d’un objet terra vectoriel (SpatVector) :

• crop(x, y) découpe une image x en prenant l’étendue de y.

• mask(x, y) découpe une image x en prenant la zone (pixels avec des valeurs non nulles ou objets vectoriels) de y. Les pixels en dehors de cette zone auront nulle comme valeur (NA dans R).

En guise d’exemple, découpons la mosaïque avec le polygone de la ville de Sherbrooke en utilisant la méthode mask. Attention, les deux sources de données doivent avoir la même projection et il faut préalablement convertir l’objet sf en objet SpatVector de terra.

## Changement de projection pour le polygone de la ville de Sherbrooke
## Application de la même projection que celle de la mosaïque
VilleSherb.EPSG4269 <- st_transform(Arrond.Union, crs(MosaicSherb))
# Convertir l'objet sf en un objet SpatVector de terra
VilleSherb.SpatVector = vect(VilleSherb.EPSG4269)
## Découpage de la mosaïque avec le polygone de la ville de Sherbrooke
MosaicSherbCrop <- terra::mask(MosaicSherb, VilleSherb.SpatVector)
MosaicSherbCrop

class       : SpatRaster 
dimensions  : 4187, 5575, 1  (nrow, ncol, nlyr)
resolution  : 9e-05, 9e-05  (x, y)
extent      : -72.25087, -71.74913, 45.24907, 45.6259  (xmin, xmax, ymin, ymax)
coord. ref. : lon/lat NAD83 (EPSG:4269) 
source(s)   : memory
varname     : f21e05_101 
name        : f21e05_101 
min value   :        126 
max value   :        390 

## Constatez ci-dessus que le nom de l'image est f21e05_101.
## Pour le changer, utilisez la fonction names()
names(MosaicSherbCrop) = "Elevation"
MosaicSherbCrop

class       : SpatRaster 
dimensions  : 4187, 5575, 1  (nrow, ncol, nlyr)
resolution  : 9e-05, 9e-05  (x, y)
extent      : -72.25087, -71.74913, 45.24907, 45.6259  (xmin, xmax, ymin, ymax)
coord. ref. : lon/lat NAD83 (EPSG:4269) 
source(s)   : memory
varname     : f21e05_101 
name        : Elevation 
min value   :       126 
max value   :       390 

## Visualisation du résultat
plot(MosaicSherbCrop)

1.3.2 Requêtes attributaires sur des images

Avant d’effectuer une requête, il est judicieux d’explorer les valeurs des pixels de l’image avec un histogramme et la fonction summary(Nom de l'image) (valeurs minimales, maximales, quartiles, moyenne et valeurs nulles – NA).

## Sommaire statistique des valeurs
summary(MosaicSherbCrop)

   Elevation    
 Min.   :126.0  
 1st Qu.:197.7  
 Median :227.6  
 Mean   :225.4  
 3rd Qu.:251.4  
 Max.   :389.9  
 NA's   :78040  

## Histogramme
hist(MosaicSherbCrop,
     main = "Mosaïque du MNA pour la ville de Sherbrooke",
     xlab = "Élévation (mètres)", ylab = "Fréquence",
     col = "lightgreen")

## Histogramme en barre de 125 à 400 avec un saut de 25 mètres 
hist(MosaicSherbCrop,
     main = "Mosaïque du MNA pour la ville de Sherbrooke",
     xlab = "Élévation (mètres)", ylab = "Fréquence",
     breaks = seq(from = 125, to = 400, by = 25),
     col = "lightgreen")

## Sélection des pixels avec une élévation d'au moins 300 mètres
MosaicSherbCrop300 = clamp(MosaicSherbCrop, lower = 300)
plot(MosaicSherbCrop300, 
     main = "Pixels avec une élévation d'au moins 300 mètres")

## Sélection des pixels avec une élévation de 200 à 300 mètres
MosaicSherbCrop200_300 = clamp(MosaicSherbCrop, lower = 200, upper = 300)
plot(MosaicSherbCrop200_300,
     main = "Pixels avec une élévation de 200 à 300 mètres")

1.4 Exportation de données spatiales de R vers des formats géographiques

1.4.1 Exportation de données vectorielles sf

Pourquoi exporter des objets sf vers différents formats géographiques?

Plusieurs méthodes d’analyse de données spatiales ne sont pas implémentées dans les logiciels de SIG comme ArcGIS Pro ou QGIS d’où l’intérêt de recourir à R ou à Python. La démarche méthodologique classique comprend alors trois étapes :

• Importer des données géographiques.

• Réaliser des analyses avancées dans R ou Python.

• Exporter les résultats finaux vers différents formats géographiques (shapefile, GeoPackage, geodatabase d’ESRI, etc.).

Trois raisons majeures motivent l’exportation des données :

• Cartographier les résultats finaux dans votre logiciel SIG préféré.

• Partager les données avec des personnes n’utilisant pas R.

• Réaliser éventuellement d’autres analyses dans votre logiciel de SIG préféré.

Dans la section 1.1, nous avons vu que la fonction st_read() du package sf permet d’importer une multitude de formats géographiques. Pour exporter avec sf, utilisez simplement la fonction st_write(). Le code ci-dessous illustre comment exporter des objets sf aux formats shapefile (shp), GeoPackage (GPKG), Keyhole Markup Language (kml) et GeoJSON. Par défaut, st_write() n’écrase pas un fichier existant; pour l’écraser, ajoutez le paramètre append = FALSE.

## Exportation au format shapefile
st_write(PointsGPS, # couche sf
         "data/chap01/export/PointsGPS.shp",  # chemin et nom du fichier
         append = FALSE, # pour écraser le fichier s'il existe
         driver = "ESRI Shapefile")

Deleting layer `PointsGPS' using driver `ESRI Shapefile'
Writing layer `PointsGPS' to data source 
  `data/chap01/export/PointsGPS.shp' using driver `ESRI Shapefile'
Writing 89 features with 2 fields and geometry type Point.

## Exportation dans une couche dans GPKG
st_write(PointsGPS, 
         dsn = "data/chap01/export/Data.gpkg", 
         layer = "PointsGPS",
         append = FALSE, 
         driver = "GPKG")

Deleting layer `PointsGPS' using driver `GPKG'
Writing layer `PointsGPS' to data source 
  `data/chap01/export/Data.gpkg' using driver `GPKG'
Writing 89 features with 2 fields and geometry type Point.

## Exportation vers un fichier KML
st_write(PointsGPS, 
         dsn = "data/chap01/export/PointsGPS.kml", 
         append = FALSE,
         driver="KML")

Writing layer `PointsGPS' to data source 
  `data/chap01/export/PointsGPS.kml' using driver `KML'
Writing 89 features with 2 fields and geometry type Point.

## Exportation vers un fichier GeoJSON
st_write(PointsGPS, 
         dsn = "data/chap01/export/PointsGPS.geojson", 
         append = FALSE,
         driver="GeoJSON")

Deleting layer not supported by driver `GeoJSON'
Deleting layer `PointsGPS' failed
Writing layer `PointsGPS' to data source 
  `data/chap01/export/PointsGPS.geojson' using driver `GeoJSON'
Updating existing layer PointsGPS
Writing 89 features with 2 fields and geometry type Point.

Le paramètre driver de la fonction st_write permet de spécifier le format du fichier. Pour obtenir la liste des formats qu’il est possible d’importer et d’exporter, tapez dans la console st_drivers() ou consultez le tableau 1.1.

Tableau 1.1: Liste des formats avec le package sf (st_drivers)

	Nom	Description	Écriture	Si vecteur	Si raster
PCIDSK	PCIDSK	PCIDSK Database File	TRUE	TRUE	TRUE
netCDF	netCDF	Network Common Data Format	TRUE	TRUE	TRUE
PDS4	PDS4	NASA Planetary Data System 4	TRUE	TRUE	TRUE
VICAR	VICAR	MIPL VICAR file	TRUE	TRUE	TRUE
JP2OpenJPEG	JP2OpenJPEG	JPEG-2000 driver based on OpenJPEG library	FALSE	TRUE	TRUE
PDF	PDF	Geospatial PDF	TRUE	TRUE	TRUE
MBTiles	MBTiles	MBTiles	TRUE	TRUE	TRUE
BAG	BAG	Bathymetry Attributed Grid	TRUE	TRUE	TRUE
EEDA	EEDA	Earth Engine Data API	FALSE	FALSE	TRUE
OGCAPI	OGCAPI	OGCAPI	FALSE	TRUE	TRUE
ESRI Shapefile	ESRI Shapefile	ESRI Shapefile	TRUE	FALSE	TRUE
MapInfo File	MapInfo File	MapInfo File	TRUE	FALSE	TRUE
UK .NTF	UK .NTF	UK .NTF	FALSE	FALSE	TRUE
LVBAG	LVBAG	Kadaster LV BAG Extract 2.0	FALSE	FALSE	TRUE
OGR_SDTS	OGR_SDTS	SDTS	FALSE	FALSE	TRUE
S57	S57	IHO S-57 (ENC)	TRUE	FALSE	TRUE
DGN	DGN	Microstation DGN	TRUE	FALSE	TRUE
OGR_VRT	OGR_VRT	VRT - Virtual Datasource	FALSE	FALSE	TRUE
Memory	Memory	Memory	TRUE	FALSE	TRUE
CSV	CSV	Comma Separated Value (.csv)	TRUE	FALSE	TRUE
GML	GML	Geography Markup Language (GML)	TRUE	FALSE	TRUE
GPX	GPX	GPX	TRUE	FALSE	TRUE
KML	KML	Keyhole Markup Language (KML)	TRUE	FALSE	TRUE
GeoJSON	GeoJSON	GeoJSON	TRUE	FALSE	TRUE
GeoJSONSeq	GeoJSONSeq	GeoJSON Sequence	TRUE	FALSE	TRUE
ESRIJSON	ESRIJSON	ESRIJSON	FALSE	FALSE	TRUE
TopoJSON	TopoJSON	TopoJSON	FALSE	FALSE	TRUE
OGR_GMT	OGR_GMT	GMT ASCII Vectors (.gmt)	TRUE	FALSE	TRUE
GPKG	GPKG	GeoPackage	TRUE	TRUE	TRUE
SQLite	SQLite	SQLite / Spatialite	TRUE	FALSE	TRUE
ODBC	ODBC		FALSE	FALSE	TRUE
WAsP	WAsP	WAsP .map format	TRUE	FALSE	TRUE
PGeo	PGeo	ESRI Personal GeoDatabase	FALSE	FALSE	TRUE
MSSQLSpatial	MSSQLSpatial	Microsoft SQL Server Spatial Database	TRUE	FALSE	TRUE
PostgreSQL	PostgreSQL	PostgreSQL/PostGIS	TRUE	FALSE	TRUE
MySQL	MySQL	MySQL	TRUE	FALSE	TRUE
OpenFileGDB	OpenFileGDB	ESRI FileGDB	TRUE	TRUE	TRUE
DXF	DXF	AutoCAD DXF	TRUE	FALSE	TRUE
CAD	CAD	AutoCAD Driver	FALSE	TRUE	TRUE
FlatGeobuf	FlatGeobuf	FlatGeobuf	TRUE	FALSE	TRUE
Geoconcept	Geoconcept	Geoconcept	TRUE	FALSE	TRUE
GeoRSS	GeoRSS	GeoRSS	TRUE	FALSE	TRUE
VFK	VFK	Czech Cadastral Exchange Data Format	FALSE	FALSE	TRUE
PGDUMP	PGDUMP	PostgreSQL SQL dump	TRUE	FALSE	TRUE
OSM	OSM	OpenStreetMap XML and PBF	FALSE	FALSE	TRUE
GPSBabel	GPSBabel	GPSBabel	TRUE	FALSE	TRUE
OGR_PDS	OGR_PDS	Planetary Data Systems TABLE	FALSE	FALSE	TRUE
WFS	WFS	OGC WFS (Web Feature Service)	FALSE	FALSE	TRUE
OAPIF	OAPIF	OGC API - Features	FALSE	FALSE	TRUE
EDIGEO	EDIGEO	French EDIGEO exchange format	FALSE	FALSE	TRUE
SVG	SVG	Scalable Vector Graphics	FALSE	FALSE	TRUE
Idrisi	Idrisi	Idrisi Vector (.vct)	FALSE	FALSE	TRUE
XLS	XLS	MS Excel format	FALSE	FALSE	TRUE
ODS	ODS	Open Document/ LibreOffice / OpenOffice Spreadsheet	TRUE	FALSE	TRUE
XLSX	XLSX	MS Office Open XML spreadsheet	TRUE	FALSE	TRUE
Elasticsearch	Elasticsearch	Elastic Search	TRUE	FALSE	TRUE
Carto	Carto	Carto	TRUE	FALSE	TRUE
AmigoCloud	AmigoCloud	AmigoCloud	TRUE	FALSE	TRUE
SXF	SXF	Storage and eXchange Format	FALSE	FALSE	TRUE
Selafin	Selafin	Selafin	TRUE	FALSE	TRUE
JML	JML	OpenJUMP JML	TRUE	FALSE	TRUE
PLSCENES	PLSCENES	Planet Labs Scenes API	FALSE	TRUE	TRUE
CSW	CSW	OGC CSW (Catalog Service for the Web)	FALSE	FALSE	TRUE
VDV	VDV	VDV-451/VDV-452/INTREST Data Format	TRUE	FALSE	TRUE
MVT	MVT	Mapbox Vector Tiles	TRUE	FALSE	TRUE
NGW	NGW	NextGIS Web	TRUE	TRUE	TRUE
MapML	MapML	MapML	TRUE	FALSE	TRUE
GTFS	GTFS	General Transit Feed Specification	FALSE	FALSE	TRUE
PMTiles	PMTiles	ProtoMap Tiles	TRUE	FALSE	TRUE
JSONFG	JSONFG	OGC Features and Geometries JSON	TRUE	FALSE	TRUE
TIGER	TIGER	U.S. Census TIGER/Line	FALSE	FALSE	TRUE
AVCBin	AVCBin	Arc/Info Binary Coverage	FALSE	FALSE	TRUE
AVCE00	AVCE00	Arc/Info E00 (ASCII) Coverage	FALSE	FALSE	TRUE
HTTP	HTTP	HTTP Fetching Wrapper	FALSE	TRUE	TRUE

1.4.2 Exportation de données raster

L’exportation d’objets SpatRasters de terra est très simple avec la méthode terra::writeRaster. En guise d’exemple, le code ci-dessous exporte la mosaïque de MNA dans un fichier GeoTIFF. Notez que le paramètre filetype permet de spécifier d’autres formats d’images de la liste qui est disponible au lien suivant : https://gdal.org/drivers/raster/index.html. En guise d’exemple, les paramètres EIR, ENVI, RST, ERS et GRASS permettent d’exporter vers les logiciels de télédétection ERDAS, ENVI, Idrisi, ERMapper et GRASS, tandis que le paramètre GPKG permet d’exporter vers un GeoPackage raster.

terra::writeRaster(MosaicSherbCrop, "data/chap01/export/MosaicSherb.tif", 
                   filetype = "GTiff", 
                   overwrite = TRUE)

1.5 Cartographie avec R

Pourquoi cartographier des données dans R?

Vous avez certainement un logiciel de SIG préféré pour construire une carte thématique (QGIS ou ArcGIS Pro par exemple). Puisqu’en quelques clics de souris, il est facile de réaliser une carte dans un SIG, quel est donc l’intérêt d’écrire des lignes de code pour afficher une carte dans R? Autrement dit, pourquoi devriez-vous vous compliquer la vie à apprendre de la syntaxe R pour produire une simple carte? Savoir cartographier dans R a plusieurs avantages :

• Cartographier rapidement les résultats d’une analyse dans R permet d’éviter des allers-retours (exportation et importation de données) entre R et un logiciel de SIG. Or, la cartographie fait partie intégrante d’une démarche méthodologique d’analyse ou de modélisation spatiale. Vous restez ainsi dans le même environnement de travail (R) jusqu’à l’obtention de vos résultats finaux. Une fois ces derniers obtenus, vous pouvez les exporter et construire une carte très élaborée dans un logiciel de SIG.

• La syntaxe R n’est pas si compliquée. Quelques lignes de code écrites pour une première analyse peuvent être réutilisées, modifiées et bonifiées pour une autre analyse. Au fil de vos projets, vous construirez des cartes de plus en plus élaborées. Autrement dit, après quelques heures d’investissement, vous deviendrez une personne experte en cartographie dans R!

Quels packages utiliser pour la cartographie dans R?

Il existe plusieurs packages R pour la cartographie, notamment :

• ggplot2 est certainement le meilleur package R pour réaliser des graphiques (Wickham 2016). Il permet désormais de construire des cartes.

• cartography permet de construire efficacement des cartes thématiques (Giraud et Lambert 2016). Pour avoir une idée de son potentiel, consultez cette Cheatsheet.

• tmap (Tennekes 2018) est actuellement l’un des packages les plus complets et les plus utilisés pour construire des cartes thématiques.

• Des packages spécifiques permettent de créer des cartes interactives sur Internet, notamment mapview, mapdeck et leaflet. Ce dernier est basé sur la librairie JavaScript, largement utilisée dans le domaine de la cartographie sur Internet.

Dans cette section, nous utilisons uniquement tmap dont plusieurs ressources sont disponibles sur Internet :

• Sur le site CRAN de tmap, une excellente vignette intitulée tmap: get started!

• Un article dans Journal of Statistical Software de Martijn Tennekes, créateur du package tmap.

• La documentation complète en PDF.

1.5.1 Manipulation des couches géométriques

1.5.1.1 Principales fonctions de représentation de couches vectorielles et matricielles

Il existe trois catégories de fonctions pour paramétrer l’affichage de couches géographiques (tableau 1.2).

Tableau 1.2: Principales fonctions pour manipuler des couches vectorielles et matricielles

Fonction	Description	Points	Lignes	Polyg.	Raster
Fonction principale
`tm_shape`	Crée un élément `tmap` à partir d'une couche géographique vectorielle (`sf`) ou matricielle (`raster`)	X	X	X	X
Fonctions de base de manipulation
`tm_polygons`	Dessine des polygones (couleur et contour)			X
`tm_symbols`	Dessine des symboles	X	X	X
`tm_lines`	Dessine des lignes		X
`tm_text`	Dessine des étiquettes à partir d'un champ	X	X	X
`tm_raster`	Affiche un raster				X
Autres fonctions de manipulation
`tm_fill`	Dessine l'intérieur de polygones			X
`tm_border`	Dessine les contours			X
`tm_bubbles`	Dessine des cercles (notamment proportionnels)	X	X	X
`tm_squares`	Dessine des carrés (notamment proportionnels)	X	X	X
`tm_dots`	Dessine des points	X	X	X
`tm_markers`	Dessine des icones avec étiquettes	X	X	X

Construction d’une carte simple avec une couche vectorielle et une couche matricielle

Le code ci-dessous permet d’afficher deux couches avec la fonction tm_shape : l’une vectorielle, l’autre matricielle (figure 1.16).

tmap_mode("plot")
# 1er objet tmap pour une couche raster
tm_shape(MosaicSherbCrop)+
  tm_raster(palette = terrain.colors(10))+
# 1er objet tmap pour une couche vectorielle
tm_shape(Arrondissements)+
  tm_borders(col = "black", lwd = 3)+ # contour noir avec une épaisseur de trois points
  tm_text("NUMERO") # Étiquettes identifiant l'arrondissement

Figure 1.16: Exemple de carte construite avec le package tmap avec une couche polygonale et une image

Ordre et hiérarchie des couches avec tmap.

Vous avez compris qu’une couche est affichée avec la fonction tm_shape et que le + permet d’ajouter une ou plusieurs fonctions d’habillage à cette couche (tm_polygons, tm_lines, tm_text, tm_raster, etc.).

Il est possible d’en superposer en utilisant plusieurs tm_shape comme suit :

tm_shape(Nom de la première couche)+ ... paramètres de la couche + tm_shape(Nom de la seconde couche)+ ... paramètres de la couche

Notez que la première couche est celle avec laquelle la projection et l’étendue de la carte sont définies. Il est toutefois possible de changer le tout en utilisant l’argument is.master = TRUE dans le tm_shape d’une couche donnée.

Construction d’une carte avec plusieurs couches vectorielles

Les lignes de code suivantes permettent de construire la figure 1.17 avec trois couches sf.

tmap_mode("plot")
## Polygones
tm_shape(Arrondissements)+
  tm_text("NUMERO")+ # Étiquettes identifiant l'arrondissement
  tm_polygons(col="wheat", border.col = "black", lwd = 3)+
## Lignes
tm_shape(Rues)+
  tm_lines(col= "gray", lwd = 1)+
## Points
tm_shape(PointsGPS.Sherb)+
  tm_dots(shape=21, col="blue", size=.3)

Figure 1.17: Exemple de carte construite avec le package tmap avec plusieurs couches vectorielles (polygones, lignes, points)

La figure 1.18 illustre la différence entre les fonctions tm_dots et tm_markers.

## Points avec tm_dots()
CartePoints <- 
  tm_shape(Arrondissements) + tm_polygons(col="wheat", border.col = "black") +
  tm_shape(PointsGPS.Sherb) + tm_dots(shape=21, col="blue", size=.3)
## Icones avec tm_markers()
CarteMarkers <- 
  tm_shape(Arrondissements) + tm_polygons(col="wheat", border.col = "black") +
  tm_shape(PointsGPS.Sherb) + tm_markers(size = 0.2, border.col = rgb(0,0,0,0))
## Combinaison des deux cartes
tmap_arrange(CartePoints, CarteMarkers, ncol=2, nrow=1)

Figure 1.18: Exemple de carte tmap avec tm_dots et tm_markers

1.5.1.2 Couleurs uniques et palette de couleurs dans tmap

Vous avez remarqué plus haut que plusieurs fonctions comprennent l’argument col pour spécifier une couleur. Pour connaître les trois manières de spécifier une couleur dans R – nom de la couleur R (lightblue par exemple), code hexadécimal (#f03b20 par exemple) ou notation RVBA (rgb(0.2, 0.4, 0.4, 0) par exemple) –, consultez la section suivante (Apparicio et Gelb 2022).

Pour spécifier une palette de couleurs sur un champ dans différentes fonctions (entre autres, tm_polygons, tm_lines, tm_fill, tm_dots), il suffit d’utiliser deux arguments dans la fonction, soit col="Nom du champ" et palette="nom de la palette de couleurs".

Le package tmap intègre les palettes de deux autres packages : viridisLite (Garnier et al. 2021) et RColorBrewer (Neuwirth 2022). Le premier propose cinq palettes de couleurs : viridis, magma, plasma, inferno, cividis. Le second intègre une série de palettes de couleurs proposées par la géographe et cartographe Cynthia Brewer et ses collègues (Harrower et Brewer 2003; Brewer, Hatchard et Harrower 2003). Vous avez probablement déjà exploré leur site Internet où il est possible de sélectionner une palette en fonction du nombre de classes, de la nature des données et de la codification des couleurs (HEX, RGB, CMYK). Succinctement, RColorBrewer propose plusieurs palettes regroupées selon trois catégories :

• Palettes qualitatives à appliquer à une variable qualitative nominale comme son nom l’indique (figure 1.19). Pour afficher les palettes et connaître leurs noms, tapez display.brewer.all(type="qual") dans la console.

• Palettes séquentielles pour une variable continue avec des valeurs faibles à fortes (figure 1.20). Tapez display.brewer.all(type="seq") dans la console.

• Palettes divergentes à appliquer à une variable continue dont les valeurs aux deux extrémités s’opposent (figure 1.21). Tapez display.brewer.all(type="div") dans la console.

Figure 1.19: Palettes de couleurs qualitatives du package RColorBrewer

Figure 1.20: Palettes de couleurs séquentielles du package RColorBrewer

Figure 1.21: Palettes de couleurs divergentes du package RColorBrewer

Comparaison de palettes avec un nombre de classes défini

Si vous connaissez le nombre de classes, mais que vous hésitez à choisir telle ou telle palette de couleurs, tapez dans la console :

• display.brewer.all(n=5, type="seq", exact.n=TRUE)
• display.brewer.all(n=5, type="div", exact.n=TRUE)
• display.brewer.all(n=5, type="qual", exact.n=TRUE)

D’autres arguments peuvent être ajoutés comme colorblindFriendly=TRUE qui renvoie uniquement des palettes de couleurs adaptées aux personnes daltoniennes. En guise d’exemple, avec cinq classes, il est possible de comparer neuf palettes divergentes et six autres adaptées aux personnes daltoniennes (figure 1.22).

Figure 1.22: Palettes de couleurs divergentes du package RColorBrewer avec cinq classes

Vous hésitez encore à choisir une palette de couleurs? Tapez la syntaxe ci-dessous dans la console pour afficher l’ensemble des palettes des packages RColorBrewer et viridisLite.

tmaptools::palette_explorer()

Pour inverser les couleurs d’une palette, vous devez précéder le nom de la palette par un signe moins (exemple : -Greens).

1.5.1.3 Cartographie d’une variable qualitative : valeurs uniques

Application à une couche de points

Le code ci-dessous illustre comment construire une carte thématique avec des couleurs appliquées à une variable qualitative nominale (champ TYPE de la couche InstallationSport) d’une couche de points (figure 1.23).

## Carte
tm_shape(Arrondissements)+
  tm_borders()+
tm_shape(InstallationSport)+
  tm_dots(shape = 21,
          size=.3,
          col= "TYPE", 
          palette = "Set1", 
          title ="Type d'installation")+
tm_layout(main.title = "Installations sportives",
          frame=FALSE,
          legend.position = c("left", "top"),
          legend.outside=TRUE)

Figure 1.23: Exemple de cartographie d’une variable qualitative sur des points

Application à une couche de lignes

Le code ci-dessous illustre comment construire une carte thématique avec des couleurs appliquées à une variable qualitative nominale (champ TYPESEGMEN) d’une couche de lignes (figure 1.24).

## Listes des valeurs uniques
table(Rues$TYPESEGMEN)

      Artère    Autoroute Chemin privé  Collectrice       Locale 
        1459          380          467          579         4844 

## Lignes
tmap_mode("plot")
tm_shape(Rues)+
  tm_lines(col= "TYPESEGMEN",
           palette = c("red", "brown4", "cornsilk1", "lightpink", "gainsboro"),
           lwd = 2 
           )

Figure 1.24: Exemple de cartographie d’une variable qualitative sur des lignes

Application à une couche de polygones

Le code ci-dessous illustre comment construire une carte thématique avec des couleurs appliquées à une variable qualitative nominale (champ SDRNOM de la couche AD2021) d’une couche de polygones (figure 1.25).

## Importation de la couche des aires de diffusion de 2021 pour la RMR de Sherbrooke
AD2021 <- st_read(dsn = "data/chap01/gpkg/Recen2021Sherbrooke.gpkg", 
                  layer = "SherbAD", 
                  quiet = TRUE)
## Carte
tmap_mode("plot")
tm_shape(AD2021)+
  tm_fill(col= "SDRNOM", 
          palette = "Set2", 
          lwd = 1, 
          title ="Municipalité")+
  tm_borders(col="black")+
tm_layout(main.title = "Aires de diffusion de 2021",
          frame =FALSE,
          legend.position = c("left", "top"),
          legend.outside=TRUE)

Figure 1.25: Exemple de cartographie d’une variable qualitative sur des polygones

1.5.1.4 Cartographie d’une variable discrète : cercles proportionnels

La syntaxe ci-dessous permet de créer une carte avec des cercles proportionnels pour les municipalités de la région administrative de l’Estrie (figure 1.26).

## Importation des municipalités (subdivisions de recensements - SDR) de l'Estrie
SDR.Estrie <- st_read(dsn = "data/chap01/gpkg/Recen2021Sherbrooke.gpkg", 
                  layer = "sdr_Estrie", quiet = TRUE)
## Importation des MRC (divisions de recensements - DR) de l'Estrie
DR.Estrie <- st_read(dsn = "data/chap01/gpkg/Recen2021Sherbrooke.gpkg", 
                  layer = "DREstrie2021",  quiet = TRUE)
## Importation des données sur la population
PopSDR <- read.csv("data/chap01/tables/SDR_Estrie.csv")
PopSDR$SDRidu <- as.character(PopSDR$SDRidu)
## Fusion des données
SDR.Estrie <- merge(SDR.Estrie, PopSDR, by.x = "SDRIDU", by.y = "SDRidu")
## Construction de la carte
tmap_mode("plot")
tm_shape(SDR.Estrie)+
  tm_polygons(col="whitesmoke", border.col = "grey30", lwd = 1)+
  tm_bubbles(size = "SDRpop_2021",
             border.col = "black",
             col = "tomato1",
             title.size = "Population",
             scale = 3)+ # facteur multiplicateur pour la taille du cercle
tm_shape(DR.Estrie)+
  tm_borders(col="black", lwd = 2)

Figure 1.26: Exemple de carte avec des cercles proportionnels

1.5.1.5 Cartographie d’une variable continue : cartes choroplèthes et méthodes de discrétisation

L’argument style, qui est commun à plusieurs fonctions (tm_polygons, tm_fill, tm_lines, tm_dots, etc.), permet de choisir une méthode de discrétisation dont les principales sont :

• fixed: intervalles fixés par l’analyste.

• equal: intervalles égaux.

• pretty: intervalles arrondis aux nombres entiers.

• quantile: selon les quantiles (même nombre d’observations dans chaque classe).

• jenks: selon la méthode de Jenks.

• sd: selon l’écart-type.

D’autres méthodes peuvent être utilisées comme kmeans, hclust, bclust, fisher, dpih, headtails et log10_pretty. En guise d’exemple, la figure 1.28 présente une discrétisation en cinq classes selon la méthode des quantiles. Notez aussi qu’il est possible de réaliser une carte avec un dégradé continu avec style = "cont" tel qu’illustré ci-dessous (figure 1.27).

## Sélection des aires de diffusion de Sherbrooke
AD2021.sherb <- subset(AD2021, SDRNOM == "Sherbrooke")
## Carte
tmap_mode("plot")
tm_shape(AD2021.sherb)+
  tm_fill(col= "HabKm2", 
          palette = "Reds",  
          style = "cont",
          title ="Hab./km2")+
  tm_borders(col="black")

Figure 1.27: Exemple de carte choroplèthe avec une palette continue

La figure 1.28 utilise une discrétisation selon la méthode de quantiles avec cinq classes. Autrement dit, chaque classe comprend 20 % des aires de diffusion de la ville de Sherbrooke.

tmap_mode("plot")
tm_shape(AD2021.sherb)+
  tm_fill(col= "HabKm2",
          palette = "Reds",  
          n = 5, # nombre de classes
          style = "quantile",
          legend.format = list(text.separator = "à"),
          title ="Hab./km2")+
  tm_borders(col="black", lwd = .5)

Figure 1.28: Exemple de carte choroplèthe avec une discrétisation selon les quantiles

La figure 1.29 présente quatre méthodes de discrétisation différentes appliquées au revenu médian des ménages par secteur de recensement dans la région métropolitaine de recensement de Sherbrooke en 2021.

Figure 1.29: Différentes méthodes de discrétisation

1.5.2 Cartes interactives

Avec la fonction tmap_mode, il est possible de choisir l’un des deux modes de visualisation suivants :

• statique avec tmap_mode("plot").
• interactif avec tmap_mode("view").

Vous constaterez ci-dessous que par défaut, trois fonds de carte sont disponibles dans la carte interactive, soit dans l’ordre Esri.WorldGrayCanvas, OpenStreetMap et Esri.WorldTopoMap.

## Mode active tmap
tmap_mode("view")
## Importation des couches
Arrond.sf = read_sf("data/chap01/shp/Arrondissements.shp")
InstallSR.sf = read_sf("data/chap01/shp/Installations_sportives_et_recreatives.shp")
## Carte
tm_shape(InstallSR.sf)+ tm_dots(size = 0.05, shape = 21, col = "red")+
tm_shape(Arrond.sf)+ tm_borders(col="black", lwd= .5)

Il est aussi possible de changer les fonds de carte avec la fonction tm_basemap tandis que la fonction tm_tiles permet de superposer une tuile (pour la toponymie par exemple) (tableau 1.3).

Tableau 1.3: Fonctions pour des cartes interactives

Fonction	Description
tmap_mode	Choisir le mode statique ou interactive
tm_basemap	Spécifier un fond de carte
tm_tiles	Spécifier une tuile de fond

Dans le code ci-dessous, nous utilisons uniquement deux fonds de carte. Remarquez les lignes avec l’argument popup.vars qui permet de définir les champs visibles dans la fenêtre surgissante (pop-up). Cliquez sur une installation sportive pour activer la fenêtre surgissante.

## Carte
tm_basemap(c("OpenStreetMap", "Esri.WorldTopoMap"))+
tm_shape(InstallSR.sf)+ 
  tm_dots(size = 0.05, shape = 21, col = "red",
          # définition pour le pop-up (clic sur une installation)
          popup.vars=c("Nom : "="NOM",
                       "Type : " = "TYPE",
                       "Éclairage : " = "ECLAIRAGE",
                       "Éclairage : " = "SURFACE"),
          id = "OBJECTID")+
tm_shape(Arrond.sf)+ tm_borders(col="black", lwd= .5)

Où trouver des fonds de carte?

Une liste des fonds de carte Leaflet est disponible au lien suivant.

1.5.3 Mise en page d’une carte

Les principales fonctions de mise en page d’une carte sont présentées au tableau 1.4.

Tableau 1.4: Fonctions d’habillage d’une carte

Fonction	Description	Principaux arguments
tm_facets	Créer un élément tmap avec plusieurs vignettes	by: groupé par colonne. nrow et ncol: nombres de lignes et de colonnes
tmap_arrange	Fusionner plusieurs cartes dans une mise en page	nrow et ncol: nombre de lignes et de colonnes
tm_grid	Ajouter une grille de lignes de coordonnées (ex. long/lat)	x et y: vecteurs pour les coordonnées
tm_credits	Créer un texte pour spéficier l’auteur.e ou la source de la carte	text: texte. size: taille du texte. fontfamily: police du texte
tm_scale_bar	Créer une échelle	break: vecteur numérique pour l’échelle. position: position de l’échelle avec les valeurs left, center, right, bottom, top. Par exemple c(‘left’, ‘bottom’)
tm_compass	Créer une flèche du nord	type: type de flèche du Nord (‘arrow’, ‘4star’, ‘8star’, ‘radar’, ‘rose’)
tm_logo	Ajouter un logo à une carte	file: chemin et nom du fichier ou URL
tm_xlab	Ajouter un titre sur l’axe des X de la carte	text: nom de l’axe
tm_ylab	Ajouter un titre sur l’axe des Y de la carte	text: nom de l’axe
tm_layout	Spécifier des éléments de mise en page de la carte	title: titre de la carte
tm_legend	Paramétrer la légende de la carte	position: position de la légende avec les valeurs left, center, right, bottom, top
tmap_options	Paramétrer et conserver plusieurs options sur la carte	unit: unités de mesures (‘imperial’, ‘km’, ‘m’, ‘mi’, and ‘ft’)

1.5.3.1 Combinaison de plusieurs cartes

Tel que décrit dans le tableau 1.4, il existe deux fonctions pour combiner deux cartes : tmap_arrange et tm_facets.

Pour ceux et celles réalisant régulièrement des graphiques dans R avec ggplot2, tmap_arrange est très similaire à la fonction ggarrange du package ggpubr qui permet de fusionner plusieurs graphiques. Globalement, le principe est le suivant : vous réalisez deux cartes ou plus que vous combinez dans une même sortie avec tmap_arrange. Vous trouverez ci-dessous un exemple avec deux cartes (figure 1.30).

tmap_mode("plot")
## Carte 1
Carte1 =  tm_shape(SDR.Estrie)+
            tm_polygons(col="whitesmoke", border.col = "grey30", lwd = 1)+
            tm_bubbles(size = "SDRpop_2021",
                       border.col = "black",
                       col = "tomato1",
                       title.size = "Population",
                       scale = 3)+ # facteur multiplicateur pour la taille du cercle
          tm_shape(DR.Estrie)+ tm_borders(col="black", lwd = 2)
## Calcul de la densité de population
SDR.Estrie$HabKm2 <- as.numeric(SDR.Estrie$SDRpop_2021 / (st_area(SDR.Estrie) / 1000000))
## Carte 2
Carte2 =  tm_shape(SDR.Estrie)+
              tm_fill(col= "HabKm2", 
                    palette = "Reds",  
                    style = "quantile", n = 4,
                    title ="Hab./km2",
                    legend.format = list(text.separator = "à"))+
              tm_borders(col="black")+
          tm_shape(DR.Estrie)+ tm_borders(col="black", lwd = 2)
## Combinaison des deux cartes
tmap_arrange(Carte1, Carte2, ncol = 2, nrow = 1)

Figure 1.30: Exemple de combinaisons de carte avec tmap_arrange

Quant à la fonction tm_facets, elle permet de créer plusieurs cartes avec l’argument by. Prenons un exemple concret : vous disposez d’une couche géographique des municipalités du Québec et vous souhaitez réaliser une carte pour chaque région administrative. L’argument by = "Region" vous permet alors d’avoir une vignette par région. Dans l’exemple ci-dessous, nous avons cartographié la même variable (densité de population) pour différentes zones de la région métropolitaine de Sherbrooke (figure 1.31).

tmap_mode("plot")
## Création d'une variable zone basée sur les noms des municipalités
AD2021$Zone <- ifelse(AD2021$SDRNOM == "Sherbrooke", "A. Sherbrooke", "") 
AD2021$Zone <- ifelse(AD2021$SDRNOM %in% c("Compton", "Waterville", "Hatley", "North Hatley"), 
                      "B. Sud", AD2021$Zone) 
AD2021$Zone <- ifelse(AD2021$SDRNOM %in% c("Orford", "Magog", "Saint-Denis-de-Brompton"), 
                      "C. Est", AD2021$Zone) 
AD2021$Zone <- ifelse(AD2021$SDRNOM %in% c("Ascot Corner", "Val-Joli", "Stoke"), 
                      "C. Nord", AD2021$Zone) 
## Création des cartes avec tm_facets
tmap_mode("plot")
tm_shape(AD2021)+
  tm_fill(col= "HabKm2",
          palette = "Reds",  
          n = 5, # nombre de classes
          style = "quantile",
          title ="Hab./km2",
          legend.format = list(text.separator = "à"))+
  tm_borders(col="black", lwd = .5)+
  tm_facets(by = "Zone")

Figure 1.31: Premier exemple de combinaison de cartes avec tm_facets

L’utilisation de tm_facets peut être également très utile pour comparer les distributions spatiales de points à différentes années (figure 1.32).

tmap_mode("plot")
## Importation des incidents
Incidents <- st_read("data/chap01/shp/IncidentsSecuritePublique.shp", quiet = TRUE)
## Création des cartes avec tm_facets
tmap_mode("plot")
tm_shape(Arrondissements) + 
  tm_polygons(col="wheat", border.col = "black") +
tm_shape(Incidents) +
  tm_dots(shape=21, col="blue", size=.2) +
tm_facets(by = "ANNEE")

Figure 1.32: Deuxième exemple de combinaisons de carte avec tm_facets

1.5.3.2 Mise en page d’une carte

Nous reprenons la figure 1.33 et l’habillons en ajoutant une échelle (tm_scale_bar), une flèche du Nord (tm_compass), la source et l’auteur (tm_credits) et un titre (tm_layout) (figure 1.33).

## Carte 1
tmap_mode("plot")
tm_shape(SDR.Estrie)+
            tm_fill(col= "HabKm2", palette = "Greens",  
                    style = "quantile", n = 4,
                    title ="Hab./km2",
                    legend.format = list(text.separator = "à"))+
            tm_bubbles(size = "SDRpop_2021", border.col = "black", col = "tomato1", scale = 3,
                       title.size = "Population")+ 
            tm_borders(col="black")+
## Ajout de de la flèche du Nord
tm_compass(position = c("right", "bottom"), 
           size = 2)+
## Ajout de l'échelle
tm_scale_bar(breaks  = c(0, 25, 50),
             position = c("right", "bottom"))+
## Ajout de la source
tm_credits("Source : recensement de 2021, Statistique Canada\nAuteur : Jéremy Lacartemplace.", 
           position = c("right", "bottom"),
           size = 0.7,
           align = "right") +
## Légende  
tm_legend(position = c("left", "top"), 
          frame = FALSE, bg.color = "white")+
## Modification de la mise en page
tm_layout(main.title = "Municipalités de l'Estrie",
          legend.outside = TRUE,
          frame = FALSE)

Figure 1.33: Habillage d’une carte

Aller plus loin avec tmap?

Nous avons abordé uniquement les principales fonctions et arguments pour l’habillage d’une carte. Plusieurs exemples de très belles cartes créées avec tmap sont disponibles aux ressources suivantes :

• L’excellente vignette intitulée tmap: get started!

• Visualizing Spatial Data in R with tmap.

• Making Maps with R.

• Le chapitre Making maps with R du livre Geocomputation with R.

1.5.4 Exportation d’une carte

Une fois la carte finalisée, il est possible de l’exporter dans différents formats avec la fonction tmap_save :

• En mode image (png, jpg, bmp, tiff) pour l’insérer dans un logiciel de traitement de texte (Word ou OpenOffice Writer) ou dans un éditeur LaTeX (Overleaf par exemple).

• En mode vectoriel (PDF ou SVG) pour finaliser l’édition de la carte dans un logiciel de création graphique vectorielle (Illustrator par exemple).

• En HTML dans lequel la carte sera intégrée selon le mode de visualisation interactive, sous la forme d’un widget Leaflet.

## Transformation en long/lat
## Carte 1
tmap_mode("plot")
Carte1 <- tm_shape(SDR.Estrie)+
  tm_fill(col= "HabKm2", palette = "Greens", style = "quantile", n = 4, title ="Hab./km2")+
  tm_bubbles(size = "SDRpop_2021", border.col = "black", col = "tomato1", scale = 3,
                       title.size = "Population")+ 
  tm_borders(col="black")+
  tm_compass(position = c("right", "bottom"), size = 2)+
  tm_scale_bar(breaks  = c(0, 25, 50), position = c("right", "bottom"))+
  tm_credits("Source : recensement de 2021, Statistique Canada\nAuteur : Jéremy Lacartemplace.", 
           position = c("right", "bottom"), size = 0.7, align = "right") +
  tm_legend(position = c("left", "top"), frame = FALSE, bg.color = "white")+
  tm_layout(main.title = "Municipalités de l'Estrie", legend.outside = TRUE, frame = FALSE)

## Exportation de la Carte1 au format png
tmap_save(Carte1, filename = "data/chap01/export/Carte1.png", dpi = 600)
## Exportation de la Carte1 au format PDF
tmap_save(Carte1, filename = "data/chap01/export/Carte1.pdf")
## Exportation de la Carte1 au format HTML
tmap_save(Carte1, filename = "data/chap01/export/Carte1.html")

1.6 Quiz de révision du chapitre

La classe sf est composée de trois éléments :

Relisez au besoin la section 1.1.1.4.1.

simple feature geometry (sfg) : géométrie d’une observation
simple feature column (sfc) : liste toutes les géométries d’une couche
data.fame : données attributaires
raster : données images

Laquelle de ces fonctions permet de changer la projection cartographique d’une couche géographique?

Relisez au besoin le début de la section 1.2.1.

st_crs(x)
st_transform(x, crs)
st_is_longlat(x)

Laquelle de ces fonctions n’est pas une fonction géométrique sur une couche?

Relisez au besoin la section 1.2.2.

st_bbox(x)
st_union(x)
st_point_on_surface(x)
st_crop(x, y, xmin, ymin, xmax, ymax)
st_centroid(x)

Comparativement à l’algorithme de Douglas et Peucker, que permet l’algorithme de Visvalingam lors de la simplification des contours?

Relisez au besoin la section 1.2.2.4.

Il est plus rapide.
Il permet de conserver les frontières.

Tous les points sont compris dans leur enveloppe convexe.

Relisez au besoin la section 1.2.2.5.

Vrai
Faux

Quelles sont les quatre fonctions de mesures géométriques et de récupération des coordonnées géographiques?

Relisez au besoin la section 1.2.4.

st_area(x)
st_length(x)
st_distance(x,y)
st_coordinates(x)
st_union(x)

Quelle est la différence entre les fonctions st_intersects(x, y) et st_intersection(x, y)?

Relisez le deuxième encadré à la section 1.2.6.

Elles génèrent le même résultat.
La première est une requête spatiale, la seconde renvoie l’intersection entre deux couches.
La première renvoie l’intersection entre deux couches, la seconde est une requête spatiale.

Laquelle des fonctions sf permet d’exporter des données vectorielles?

Relisez au besoin la section 1.4.1.

st_read()
st_write()
writeRaster()

1.7 Exercices de révision

Exercice 1. Découpage des rues de l’arrondissement des Nations de la ville de Sherbrooke

Complétez le code ci-dessous avec les étapes suivantes :

• Requête attributaire pour créer un objet sf avec uniquement l’arrondissement des Nations à partir de la couche Arrondissements et le champ NOM (voir la section 1.2.7.4).

• Découpez les rues (Rues) sur le nouvel objet sf (voir la section 1.2.3).

library(sf)
## Importation des deux couches
Arrond <- st_read("data/chap01/shp/Arrondissements.shp", quiet = TRUE)
Rues <- st_read("data/chap01/shp/Segments_de_rue.shp", quiet = TRUE)
## Requête attributaire : création d'un objet sf pour l'arrondissement des Nations
table(Arrond$NOM)
Arrond.DesNations <- subset(À compléter)
## Découper les rues avec le polygone de l'arrondissement des Nations
Rues.DesNations <- À compléter

Correction à la section 12.1.1.

Exercice 2. Calcul d’un nouveau champ

Calculez un nouveau champ (DistHVKM) dans la couche des aires de diffusion (AD) (AD.RMRSherb) qui représente la distance en kilomètres entre l’hôtel de ville de Sherbrooke et les points des AD. Puis, cartographiez le champ DistHVKM en quatre classes selon la méthode de discrétisation par quantiles. Complétez le code ci-dessous avec les étapes suivantes :

• Ajoutez un champ pour la distance (DistHVKM) dans la couche AD.RMRSherb (voir la section 1.2.4).

• Cartographiez le champ DistHVKM en quatre classes selon la méthode des quantiles (voir la section 1.5.1.5).

library(sf)
library(tmap)
## Importation des deux couches
AD.RMRSherb <- st_read(dsn = "data/chap01/gpkg/Recen2021Sherbrooke.gpkg", 
                       layer = "SherbAD", quiet = TRUE)
HotelVille <- data.frame(ID = 1, Nom = "Hôtel de ville",
                         lon = -71.89306, lat = 45.40417)
HotelVille <- st_as_sf(HotelVille, coords = c("lon","lat"), crs = 4326)
## Changement de projection avant de s'assurer que les deux couches ont la même
HotelVille <- st_transform(HotelVille, st_crs(AD.RMRSherb))
## Ajout d'un champ pour la distance en km à l'hôtel de ville pour les secteurs de recensement
AD.RMRSherb$DistHVKM <- À compléter
## Cartographie en quatre classes selon les quantiles
tmap_mode("plot")
tm_shape(À compléter)+
  tm_fill(À compléter)+
  tm_borders(col="black")

Correction à la section 12.1.2.

Exercice 3. Importation d’une couche shapefile

Importez une couche shapefile pour les divisions de recensement et calculez la densité de population (nombre d’habitants au km²). Complétez le code ci-dessous avec les étapes suivantes :

• Faites une jointure attributaire entre la couche DR.Qc et la table DR.Data (voir la section 1.2.7.2).

• Calculez le champ HabKm2, soit la division entre les champs DRpop_2021 et SUPTERRE (voir la section 1.5.1.5).

library(sf)
## Importation de la couche des divisions de recensement du Québec
DR.Qc <- st_read(dsn = "data/chap01/gpkg/Recen2021Sherbrooke.gpkg", 
                 layer = "DivisionsRecens2021", quiet = TRUE)
## Importation du fichier csv des divisions de recensement
DR.Data <- read.csv("data/chap01/tables/DRQC2021.csv")
## Jointure attributaire avec le champ IDUGD
DR.Qc <- A compléter
## Il y a déjà deux champs dans la table pour calculer la densité de population :
## SUPTERRE : superficie en km2
## DRpop_2021 : population en 2021
DR.Qc$HabKm2 <- A compléter
head(DR.Qc, n=2)
summary(DR.Qc$HabKm2)

Correction à la section 12.1.3.

Exercice 4. Coordonnées géographiques

Vous recevez les coordonnées en degrés (WGS84, EPSG : 4326) : -71.91688, 45.37579. Créez un point pour cette localisation et calculez la distance la séparant du tronçon autoroutier le plus proche. Complétez le code ci-dessous avec les étapes suivantes :

• Faites une requête attributaire pour créer un objet sf avec uniquement les tronçons autoroutiers à partir de la couche Rues et le champ TYPESEGMEN (voir la section 1.2.7.4).

• Trouvez l’identifiant du tronçon le plus proche avec la fonction st_nearest_feature (voir la section 1.2.6).

library(sf)
## Importation du réseau de rues
Rues <- st_read("data/chap01/shp/Segments_de_rue.shp", quiet=TRUE)
unique(Rues$TYPESEGMEN)
## Sélection des tronçons autoroutiers
Autoroutes <- À compléter
## Création d'une couche sf pour le point avec les coordonnées
## en degrés (WGS84, EPSG : 4326) : -71.91688, 45.37579
Point1_sf <- À compléter
## Changement de projection avant de s'assurer que les deux couches ont la même
Point1_sf <- st_transform(Point1_sf, st_crs(Autoroutes))
## Trouver le tronçon autoroutier le plus proche avec la fonction st_nearest_feature
PlusProche <- À compléter
print(PlusProche)
Point1_sf$AutoroutePlusProche <- as.numeric(st_distance(Point1_sf,
                                                        Autoroutes[PlusProche,]))
cat("Distance à l'autoroute la plus proche :", Point1_sf$AutoroutePlusProche, "m.")
## Zone tampon
ZoneTampon <- st_buffer(Point1_sf, Point1_sf$AutoroutePlusProche)
## Cartographie
tmap_mode("view")
tm_shape(ZoneTampon)+
  tm_borders(col= "black")+
tm_shape(Autoroutes)+
  tm_lines(col="red")+
tm_shape(Point1_sf)+
  tm_dots(col= "blue", shape=21, size = .2)

Correction à la section 12.1.4.

Apparicio, Philippe et Jérémy Gelb. 2022. Méthodes quantitatives en sciences sociales : un grand bol d’R. FabriqueREL, Licence CC BY-SA. https://serieboldr.github.io/MethodesQuantitatives/.

Bivand, Roger, Edzer Pebesma et Virgilio Gomez-Rubio. 2013. Applied spatial data analysis with R, Second edition. Springer, New York. https://asdar-book.org/.

Brewer, Cynthia A, Geoffrey W Hatchard et Mark A Harrower. 2003. « ColorBrewer in print: a catalog of color schemes for maps. » Cartography and geographic information science 30 (1): 5‑32. https://doi.org/10.1559/152304003100010929.

Douglas, David H et Thomas K Peucker. 1973. « Algorithms for the reduction of the number of points required to represent a digitized line or its caricature. » Cartographica: the international journal for geographic information and geovisualization 10 (2): 112‑122. https://doi.org/10.3138/FM57-6770-U75U-7727.

Garnier, Simon, Noam Ross, Robert Rudis, Antônio Pedro Camargo, Marco Sciaini et Cédric Scherer. 2021. viridis - Colorblind-Friendly Color Maps for R. s.n. https://sjmgarnier.github.io/viridis/.

Giraud, Timothée et Nicolas Lambert. 2016. « cartography: Create and Integrate Maps in your R Workflow. » JOSS 1 (4). The Open Journal. https://doi.org/10.21105/joss.00054.

Harrower, Mark et Cynthia A Brewer. 2003. « ColorBrewer.org: an online tool for selecting colour schemes for maps. » The Cartographic Journal 40 (1): 27‑37. http://dx.doi.org/10.1179/000870403235002042.

Hijmans, Robert J. 2022a. raster: Geographic Data Analysis and Modeling. R package version 3.5-15. https://CRAN.R-project.org/package=raster.

———. 2022b. terra: Spatial Data Analysis. s.n. https://CRAN.R-project.org/package=terra.

Neuwirth, Erich. 2022. RColorBrewer: ColorBrewer Palettes. s.n. https://CRAN.R-project.org/package=RColorBrewer.

Pebesma, Edzer. 2018. « Simple Features for R: Standardized Support for Spatial Vector Data. » The R Journal 10 (1): 439‑446. https://doi.org/10.32614/RJ-2018-009.

Pebesma, Edzer et Roger Bivand. 2005. « Classes and methods for spatial data in R. » R News 5 (2): 9‑13. https://CRAN.R-project.org/doc/Rnews/.

Tennekes, Martijn. 2018. « tmap: Thematic Maps in R. » Journal of Statistical Software 84 (6): 1‑39. https://doi.org/10.18637/jss.v084.i06.

Visvalingam, Maheswari et James D Whyatt. 1993. « Line generalisation by repeated elimination of points. » The cartographic journal 30 (1): 46‑51. https://doi.org/10.3138/FM57-6770-U75U-7727.

Wickham, Hadley. 2016. ggplot2: Elegant Graphics for Data Analysis. Springer-Verlag New York. https://ggplot2.tidyverse.org.